Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Neumaier, A.
1981.
Geometries and Groups.
Vol. 893,
Issue. ,
p.
223.
Neumaier, A.
1982.
Algebraic and Geometric Combinatorics.
Vol. 65,
Issue. ,
p.
305.
1985.
Annals of Discrete Mathematics (27): Cycles in Graphs.
Vol. 115,
Issue. ,
p.
351.
Perkel, Manley
1985.
Rank 4 groups with a 3-transitive suborbit.
Journal of Combinatorial Theory, Series A,
Vol. 39,
Issue. 2,
p.
226.
Ivanov, A.A.
1987.
On 2-Transitive Graphs of Girth 5.
European Journal of Combinatorics,
Vol. 8,
Issue. 4,
p.
393.
Ivanov, A. A.
and
Shpectorov, S. V.
1994.
Investigations in Algebraic Theory of Combinatorial Objects.
Vol. 84,
Issue. ,
p.
417.
Ivanov, A.A.
and
Praeger, Cheryl E.
1998.
On Locally Projective Graphs of Girth 5.
Journal of Algebraic Combinatorics,
Vol. 7,
Issue. 3,
p.
259.
Perkel, Manley
Praeger, Cheryl E.
and
Weiss, Richard
2001.
On Narrow Hexagonal Graphs with a 3-Homogeneous Suborbit.
Journal of Algebraic Combinatorics,
Vol. 13,
Issue. 3,
p.
257.
Zhou, Sanming
2007.
Graph Theory in Paris.
p.
375.
Seress, Ákos
2008.
Horizons of Combinatorics.
Vol. 17,
Issue. ,
p.
179.
Zhou, Sanming
2010.
Trivalent 2-Arc Transitive Graphs of Type $${G^1_2}$$ are Near Polygonal.
Annals of Combinatorics,
Vol. 14,
Issue. 3,
p.
397.
Swartz, Eric
2010.
A construction of an infinite family of 2-arc transitive polygonal graphs of arbitrary odd girth.
Journal of Combinatorial Theory, Series A,
Vol. 117,
Issue. 6,
p.
783.
Abiad, A.
van Dam, E.R.
and
Fiol, M.A.
2016.
Some spectral and quasi-spectral characterizations of distance-regular graphs.
Journal of Combinatorial Theory, Series A,
Vol. 143,
Issue. ,
p.
1.
Anagnostopoulou-Merkouri, Marina
and
Cameron, Peter J.
2023.
Association schemes with given stratum dimensions: on a paper of Peter M. Neumann.
Algebraic Combinatorics,
Vol. 6,
Issue. 5,
p.
1189.
Liu, Zheng-Hao
Meng, Yu
Wu, Yu-Ze
Hao, Ze-Yan
Xu, Zhen-Peng
Ai, Cheng-Jun
Wei, Hai
Wen, Kai
Chen, Jing-Ling
Ma, Jie
Xu, Jin-Shi
Li, Chuan-Feng
and
Guo, Guang-Can
2025.
Exploring the boundary of quantum correlations with a time-domain optical processor.
Science Advances,
Vol. 11,
Issue. 5,
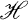 ,
, 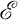 ) consisting of a graph
) consisting of a graph 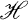 which is regular, connected and has girth m for some m ≧ 3, and a set
which is regular, connected and has girth m for some m ≧ 3, and a set 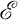 of m-gons of
of m-gons of 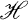 such that every 2-claw of
such that every 2-claw of 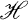 is contained in an unique element of
is contained in an unique element of 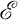 (See Section 2 for the définitions of the terms used here.) If
(See Section 2 for the définitions of the terms used here.) If 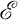 is the set of all m-gons of
is the set of all m-gons of 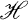 , so that there is in
, so that there is in 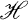 an unique m-gon on every one of its 2-claws, then we write
an unique m-gon on every one of its 2-claws, then we write 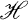 for (
for (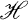 ,
, 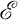 ) and call
) and call 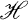 a strict polygonal graph. If we wish to emphasize the integer m, then we call (
a strict polygonal graph. If we wish to emphasize the integer m, then we call (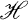 ,
, 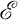 ) an m-gon-graph (respectively, a strict m-gon-graph).
) an m-gon-graph (respectively, a strict m-gon-graph).
