Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Auscher, Pascal
and
Hytönen, Tuomas
2013.
Orthonormal bases of regular wavelets in spaces of homogeneous type.
Applied and Computational Harmonic Analysis,
Vol. 34,
Issue. 2,
p.
266.
Conde, Jose M.
2013.
A note on dyadic coverings and nondoubling Calderón–Zygmund theory.
Journal of Mathematical Analysis and Applications,
Vol. 397,
Issue. 2,
p.
785.
Volberg, A L
and
Èiderman, V Ya
2013.
Non-homogeneous harmonic analysis: 16 years of development.
Russian Mathematical Surveys,
Vol. 68,
Issue. 6,
p.
973.
Вольберг, Александр Львович
Vol'berg, Alexander L'vovich
Эйдерман, Владимир Яковлевич
and
Eiderman, Vladimir Yakovlevich
2013.
Неоднородный гармонический анализ: 16 лет развития.
Успехи математических наук,
Vol. 68,
Issue. 6(414),
p.
3.
Yonghui, Cao
and
Jiang, Zhou
2013.
Morrey Spaces for Nonhomogeneous Metric Measure Spaces.
Abstract and Applied Analysis,
Vol. 2013,
Issue. ,
p.
1.
Yang, Dachun
Yang, Dongyong
and
Hu, Guoen
2013.
The Hardy Space H1 with Non-doubling Measures and Their Applications.
Vol. 2084,
Issue. ,
p.
483.
Fu, Xing
Yang, Dachun
and
Yuan, Wen
2014.
GENERALIZED FRACTIONAL INTEGRALS AND THEIR COMMUTATORS OVER NON-HOMOGENEOUS METRIC MEASURE SPACES.
Taiwanese Journal of Mathematics,
Vol. 18,
Issue. 2,
Zhou, Jiang
and
Wang, Dinghuai
2014.
Lipschitz Spaces and Fractional Integral Operators Associated with Nonhomogeneous Metric Measure Spaces.
Abstract and Applied Analysis,
Vol. 2014,
Issue. ,
p.
1.
Lin, HaiBo
and
Yang, DaChun
2014.
Equivalent boundedness of Marcinkiewicz integrals on non-homogeneous metric measure spaces.
Science China Mathematics,
Vol. 57,
Issue. 1,
p.
123.
Zheng, Taotao
Tao, Xiangxing
and
Wu, Xiaomei
2014.
Bilinear Calderón-Zygmund operators of type "Equation missing" on non-homogeneous space.
Journal of Inequalities and Applications,
Vol. 2014,
Issue. 1,
Fu, Xing
Yang, Dachun
and
Yang, Dongyong
2014.
The molecular characterization of the Hardy space H1 on non-homogeneous metric measure spaces and its application.
Journal of Mathematical Analysis and Applications,
Vol. 410,
Issue. 2,
p.
1028.
Tan, ChaoQiang
and
Li, Ji
2015.
Littlewood-Paley theory on metric spaces with non doubling measures and its applications.
Science China Mathematics,
Vol. 58,
Issue. 5,
p.
983.
Stempak, Krzysztof
2015.
ON SOME STRUCTURAL PROPERTIES OF SPACES OF HOMOGENEOUS
TYPE.
Taiwanese Journal of Mathematics,
Vol. 19,
Issue. 2,
Lu, Guanghui
and
Tao, Shuangping
2015.
Boundedness of Commutators of Marcinkiewicz Integrals on Nonhomogeneous Metric Measure Spaces.
Journal of Function Spaces,
Vol. 2015,
Issue. ,
p.
1.
Aimar, Hugo
Carena, Marilina
and
Iaffei, Bibiana
2015.
Gradual doubling property of Hutchinson orbits.
Czechoslovak Mathematical Journal,
Vol. 65,
Issue. 1,
p.
191.
Fu, Xing
Lin, HaiBo
Yang, DaChun
and
Yang, DongYong
2015.
Hardy spaces H p over non-homogeneous metric measure spaces and their applications.
Science China Mathematics,
Vol. 58,
Issue. 2,
p.
309.
Yonghui, Cao
and
Jiang, Zhou
2015.
The boundedness of Marcinkiewicz integrals commutators on non-homogeneous metric measure spaces.
Journal of Inequalities and Applications,
Vol. 2015,
Issue. 1,
Lu, Guanghui
and
Tao, Shuangping
2016.
Fractional type Marcinkiewicz integrals over non-homogeneous metric measure spaces.
Journal of Inequalities and Applications,
Vol. 2016,
Issue. 1,
Gong, Huajun
Xie, Rulong
and
Xu, Chen
2016.
Multilinear fractional integral operators on non-homogeneous metric measure spaces.
Journal of Inequalities and Applications,
Vol. 2016,
Issue. 1,
Fu, Xing
and
Zhao, Ji Man
2016.
Endpoint estimates of generalized homogeneous Littlewood–Paley g-functions over non-homogeneous metric measure spaces.
Acta Mathematica Sinica, English Series,
Vol. 32,
Issue. 9,
p.
1035.
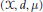 $\left( \text{ }\!\!\chi\!\!\text{ ,}\,d,\,\mu\right)$ be a separable metric measure space satisfying the known upper doubling condition, the geometrical doubling condition, and the non-atomic condition that
$\left( \text{ }\!\!\chi\!\!\text{ ,}\,d,\,\mu\right)$ be a separable metric measure space satisfying the known upper doubling condition, the geometrical doubling condition, and the non-atomic condition that 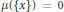 $\mu \left( \left\{ x \right\} \right)\,=\,0$ for all
$\mu \left( \left\{ x \right\} \right)\,=\,0$ for all 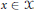 $x\,\in \,\text{ }\!\!\chi\!\!\text{ }$ . In this paper, we show that the boundedness of a Calderón–Zygmund operator
$x\,\in \,\text{ }\!\!\chi\!\!\text{ }$ . In this paper, we show that the boundedness of a Calderón–Zygmund operator 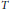 $T$ on
$T$ on 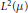 ${{L}^{2}}\left( \mu\right)$ is equivalent to that of
${{L}^{2}}\left( \mu\right)$ is equivalent to that of 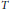 $T$ on
$T$ on 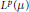 ${{L}^{p}}\left( \mu\right)$ for some
${{L}^{p}}\left( \mu\right)$ for some 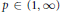 $p\,\in \,\left( 1,\,\infty\right)$ , and that of
$p\,\in \,\left( 1,\,\infty\right)$ , and that of 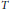 $T$ from
$T$ from 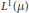 ${{L}^{1}}\left( \mu\right)$ to
${{L}^{1}}\left( \mu\right)$ to 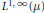 ${{L}^{1,\,\infty }}\left( \mu\right)$ . As an application, we prove that if
${{L}^{1,\,\infty }}\left( \mu\right)$ . As an application, we prove that if 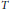 $T$ is a Calderón–Zygmund operator bounded on
$T$ is a Calderón–Zygmund operator bounded on 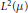 ${{L}^{2}}\left( \mu\right)$ , then its maximal operator is bounded on
${{L}^{2}}\left( \mu\right)$ , then its maximal operator is bounded on 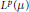 ${{L}^{p}}\left( \mu\right)$ for all
${{L}^{p}}\left( \mu\right)$ for all 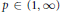 $p\,\in \,\left( 1,\,\infty\right)$ and from the space of all complex-valued Borel measures on
$p\,\in \,\left( 1,\,\infty\right)$ and from the space of all complex-valued Borel measures on 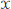 $\text{ }\!\!\chi\!\!\text{ }$ to
$\text{ }\!\!\chi\!\!\text{ }$ to 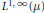 ${{L}^{1,\,\infty }}\left( \mu\right)$ . All these results generalize the corresponding results of Nazarov et al. on metric spaces with measures satisfying the so-called polynomial growth condition.
${{L}^{1,\,\infty }}\left( \mu\right)$ . All these results generalize the corresponding results of Nazarov et al. on metric spaces with measures satisfying the so-called polynomial growth condition.
