No CrossRef data available.
Article contents
Biplanar Surfaces of Order Three II
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
A surface of order three F in the real projective three-space P 3 is met by every line, not in F, in at most three points. F is biplanar if it contains exactly one non-differentiable point v and the set of tangents of F at v is the union of two distinct planes, say τ 1 and τ 2.
In [2], we examined the biplanar surfaces containing the line τ 1 ⌒ τ 2. In the present paper, we classify and describe the biplanar F with the property that τ1 ⌒ τ 2⌒ F = {v}.
We denote the planes, lines and points of P 3 by the letters α, β, …, L, M, … and p, q, … respectively. For a collection of flats α, L, p, …, 〈α, L, p, …〉 denotes the flat of P 3 spanned by them. For a set M in P 3,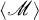 
denotes the flat of P 3 spanned by the points of 
.
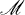Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1980
References
1.
Bisztriczky, T., Surfaces of order three with a peak. I,
J. of Geometry,
11 (1978), 55–83.Google Scholar
2.
Bisztriczky, T., Biplanar surfaces of order three,
Can. J. Math.
31 (1979), 396–418.Google Scholar
4.
Blythe, W. H., On modules of cubic surfaces (Cambridge University Press, London, 1905).Google Scholar
5.
Marchand, A., Sur les propriétés différentielles du premier ordre des surfaces simples de Jordan et quelques applications,
Ann. Ec. Norm. Sup.
63 (1947), 81–108.Google Scholar
You have
Access