Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rubin, Matatyahu
1979.
On the automorphism groups of homogeneous and saturated Boolean algebras.
Algebra Universalis,
Vol. 9,
Issue. 1,
p.
54.
Rubin, Matatyahu
1980.
On the automorphism groups of countable Boolean algebras.
Israel Journal of Mathematics,
Vol. 35,
Issue. 1-2,
p.
151.
Rubin, Matatyahu
1980.
On the reconstruction of boolean algebras from their automorphism groups.
Archiv für Mathematische Logik und Grundlagenforschung,
Vol. 20,
Issue. 3-4,
p.
125.
van Douwen, Eric K.
Monk, J. Donald
and
Rubin, Matatyahu
1980.
Some questions about Boolean algebras.
algebra universalis,
Vol. 11,
Issue. 1,
p.
220.
Morozov, A. S.
1983.
Groups of recursive automorphisms of contructive boolean algebras.
Algebra and Logic,
Vol. 22,
Issue. 2,
p.
95.
Morozov, A. S.
1986.
Automorphisms of constructivizations of Boolean algebras.
Siberian Mathematical Journal,
Vol. 26,
Issue. 4,
p.
555.
Remmel, Jeffrey B.
1987.
Recursively rigid Boolean algebras.
Annals of Pure and Applied Logic,
Vol. 36,
Issue. ,
p.
39.
Morozov, A. S.
1988.
Permutations and implicit definability.
Algebra and Logic,
Vol. 27,
Issue. 1,
p.
12.
Morozov, A. S.
1990.
Recursive automorphisms of atomic Boolean algebras.
Algebra and Logic,
Vol. 29,
Issue. 4,
p.
310.
Dauletbaev, B. K.
1993.
Determining an atmic Boolean algebra from the action of the automorphism group.
Siberian Mathematical Journal,
Vol. 34,
Issue. 6,
p.
1041.
Nation, J. B.
1994.
J�nsson's contributions to lattice theory.
Algebra Universalis,
Vol. 31,
Issue. 3,
p.
430.
1998.
Handbook of Recursive Mathematics - Volume 1: Recursive Model Theory.
Vol. 138,
Issue. ,
p.
311.
Combarro, E. F.
2004.
On Classifying Subsets of Natural Numbers by Their Computable Permutations.
Siberian Mathematical Journal,
Vol. 45,
Issue. 1,
p.
125.
Chubb, Jennifer
Harizanov, Valentina S.
Morozov, Andrei S.
Pingrey, Sarah
and
Ufferman, Eric
2008.
Partial automorphism semigroups.
Annals of Pure and Applied Logic,
Vol. 156,
Issue. 2-3,
p.
245.
Patel, Priyam
and
Vlamis, Nicholas
2018.
Algebraic and topological properties of big mapping class groups.
Algebraic & Geometric Topology,
Vol. 18,
Issue. 7,
p.
4109.
Mashevitzky, G.
Plotkin, B.
and
Plotkin, E.
2018.
Action of endomorphism semigroups on definable sets.
International Journal of Algebra and Computation,
Vol. 28,
Issue. 08,
p.
1585.
Domat, George
Hoganson, Hannah
and
Kwak, Sanghoon
2025.
Generating Sets and Algebraic Properties of Pure Mapping Class Groups of Infinite Graphs.
Annales Henri Lebesgue,
Vol. 8,
Issue. ,
p.
373.

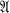 (or
(or 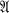 . In particular, for which algebras can one conclude that if Aut
. In particular, for which algebras can one conclude that if Aut 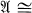 Aut
Aut 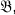 , then
, then 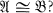 Monk has conjectured [
Monk has conjectured [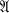 and
and 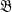 are denumerable, if each has at least one atom, and if the sum of the atoms exists in
are denumerable, if each has at least one atom, and if the sum of the atoms exists in 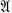 . In fact, under those assumptions the algebra 21 can be rather neatly recovered from its abstract automorphism group.
. In fact, under those assumptions the algebra 21 can be rather neatly recovered from its abstract automorphism group.