Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Leung, Y.
1979.
Robertson’s conjecture on the coefficients of close-to-convex functions.
Proceedings of the American Mathematical Society,
Vol. 76,
Issue. 1,
p.
89.
Arora, Vibhuti
Ponnusamy, Saminathan
and
Sahoo, Swadesh Kumar
2019.
Successive coefficients for spirallike and related functions.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 113,
Issue. 4,
p.
2969.

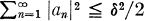 if
if 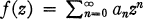 is analytic for |
is analytic for |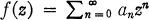
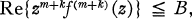
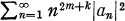
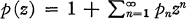 be analytic for
be analytic for 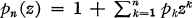 and
and 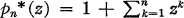 .
.