No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
The 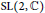 $\text{SL}\left( 2,\mathbb{C} \right)$-representation varieties of punctured surfaces form natural families parameterized by monodromies at the punctures. In this paper, we compute the loci where these varieties are singular for the cases of one-holed and two-holed tori and the four-holed sphere. We then compute the de Rham cohomologies of these varieties of the one-holed torus and the four-holed sphere when the varieties are smooth via the Grothendieck theorem. Furthermore, we produce the explicit Gauß-Manin connection on the natural family of the smooth
$\text{SL}\left( 2,\mathbb{C} \right)$-representation varieties of punctured surfaces form natural families parameterized by monodromies at the punctures. In this paper, we compute the loci where these varieties are singular for the cases of one-holed and two-holed tori and the four-holed sphere. We then compute the de Rham cohomologies of these varieties of the one-holed torus and the four-holed sphere when the varieties are smooth via the Grothendieck theorem. Furthermore, we produce the explicit Gauß-Manin connection on the natural family of the smooth 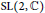 $\text{SL}\left( 2,\mathbb{C} \right)$-representation varieties of the one-holed torus.
$\text{SL}\left( 2,\mathbb{C} \right)$-representation varieties of the one-holed torus.