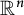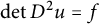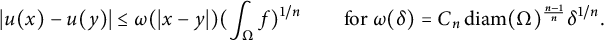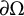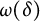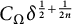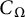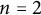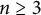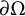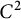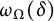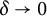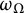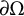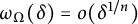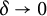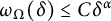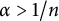1 Introduction
Alexandrov’s estimate states that if
![]() $\Omega $
is a bounded open convex domain in
$\Omega $
is a bounded open convex domain in
![]() $\mathbb {R}^n$
, and
$\mathbb {R}^n$
, and
![]() $u:\bar \Omega \to \mathbb {R}$
is a convex function such that
$u:\bar \Omega \to \mathbb {R}$
is a convex function such that
![]() $u=0$
on
$u=0$
on
![]() $\partial \Omega $
, then there exists a constant
$\partial \Omega $
, then there exists a constant
![]() $C_n$
such that
$C_n$
such that
Here,
 $$ \begin{align} [u]_\alpha := \sup_{x,y\in \Omega, x\ne y } \frac{|u(x)-u(y)|}{|x-y|^\alpha}, \end{align} $$
$$ \begin{align} [u]_\alpha := \sup_{x,y\in \Omega, x\ne y } \frac{|u(x)-u(y)|}{|x-y|^\alpha}, \end{align} $$
and
![]() $\partial u$
denotes the subgradient of u, whose definition is recalled in (2.1). For now, we just mention that if u is
$\partial u$
denotes the subgradient of u, whose definition is recalled in (2.1). For now, we just mention that if u is
![]() $C^2$
, then
$C^2$
, then
![]() $|\partial u(\Omega )| = \|\! \det D^2 u\|_{L^1(\Omega )}$
.
$|\partial u(\Omega )| = \|\! \det D^2 u\|_{L^1(\Omega )}$
.
Estimate (1.1) plays an important role in the regularity theory of the Monge-Ampère equation (see, for example [Reference Gutiérrez4, Reference Figalli2]), and it is a key ingredient in some basic linear elliptic PDE estimates (see, for example, [Reference Gilbarg and Trudinger3], Chapter 9).
In this paper, we establish some improvements of (1.1). Before stating them, we introduce some notation. We will write
and
 $$ \begin{align} \omega_\Omega(\delta):= \sup\left\{ \frac{ |u(x) - u(y)|}{|\partial u(\Omega)|^{1/n}} : u\in {C^\mathrm{con}_0}(\bar \Omega), \, u\text{ nonzero, }\ \ x,y\in \bar \Omega, \, \ |x-y|\le \delta \right\}. \end{align} $$
$$ \begin{align} \omega_\Omega(\delta):= \sup\left\{ \frac{ |u(x) - u(y)|}{|\partial u(\Omega)|^{1/n}} : u\in {C^\mathrm{con}_0}(\bar \Omega), \, u\text{ nonzero, }\ \ x,y\in \bar \Omega, \, \ |x-y|\le \delta \right\}. \end{align} $$
The definition immediately implies that for every
![]() $u\in {C^\mathrm{con}_0}(\bar \Omega )$
,
$u\in {C^\mathrm{con}_0}(\bar \Omega )$
,
 $$ \begin{align} [ u]_{\omega_\Omega} := \sup_{x,y\in \Omega, x\ne y }\frac{|u(x) - u(y)|}{\omega_\Omega(|x-y|) } \le |\partial u(\Omega)| ^{1/n} \end{align} $$
$$ \begin{align} [ u]_{\omega_\Omega} := \sup_{x,y\in \Omega, x\ne y }\frac{|u(x) - u(y)|}{\omega_\Omega(|x-y|) } \le |\partial u(\Omega)| ^{1/n} \end{align} $$
and that this is sharp in that it fails for some
![]() $u\in {C^\mathrm{con}_0}(\bar \Omega )$
if
$u\in {C^\mathrm{con}_0}(\bar \Omega )$
if
![]() $\omega _\Omega $
is replaced by any smaller function. With this notation, Alexandrov’s estimate (1.1) amounts to the assertion that
$\omega _\Omega $
is replaced by any smaller function. With this notation, Alexandrov’s estimate (1.1) amounts to the assertion that
![]() $\omega _\Omega (\delta )\le C(\Omega )\delta ^{1/n}$
for all
$\omega _\Omega (\delta )\le C(\Omega )\delta ^{1/n}$
for all
![]() $\delta>0$
.
$\delta>0$
.
In this paper, we give a precise description of
![]() $\omega _\Omega $
, depending on the geometry of
$\omega _\Omega $
, depending on the geometry of
![]() $\partial \Omega $
. This allows us to show that for any bounded, convex domain
$\partial \Omega $
. This allows us to show that for any bounded, convex domain
![]() $\Omega $
whose boundary satisfies a very weak nondegeneracy condition (see (1.12)), there exists some
$\Omega $
whose boundary satisfies a very weak nondegeneracy condition (see (1.12)), there exists some
![]() $\alpha>1/n$
such that
$\alpha>1/n$
such that
![]() $\omega _\Omega (\delta ) \le C(\Omega ,\alpha )\delta ^\alpha $
for all
$\omega _\Omega (\delta ) \le C(\Omega ,\alpha )\delta ^\alpha $
for all
![]() $\delta>0$
or, in other words, that
$\delta>0$
or, in other words, that
Beyond that, we aim to characterize the range of
![]() $\alpha $
for which an estimate like the above holds and to estimate the optimal constant
$\alpha $
for which an estimate like the above holds and to estimate the optimal constant
![]() $C(\alpha ,\Omega )$
in (1.5), in terms of the geometry of
$C(\alpha ,\Omega )$
in (1.5), in terms of the geometry of
![]() $\partial \Omega $
.
$\partial \Omega $
.
Our first result addresses domains for which the Gaussian curvature
![]() $\kappa $
of the boundary satisfies
$\kappa $
of the boundary satisfies
Except where stated otherwise, we do not impose any smoothness conditions beyond those that follow from convexity, which imply that
![]() $\partial \Omega $
is twice differentiable, and hence, the Gaussian curvature is defined,
$\partial \Omega $
is twice differentiable, and hence, the Gaussian curvature is defined,
![]() $\mathcal {H}^{n-1}$
a.e.. The left-hand side of (1.6) should be understood to mean the infimum over all points at which
$\mathcal {H}^{n-1}$
a.e.. The left-hand side of (1.6) should be understood to mean the infimum over all points at which
![]() $\kappa $
is defined.
$\kappa $
is defined.
Theorem 1.1 Assume that
![]() $\Omega \subset \mathbb {R}^n$
is convex and bounded and that (1.6) holds. Let
$\Omega \subset \mathbb {R}^n$
is convex and bounded and that (1.6) holds. Let
![]() $\alpha _* := \frac 12 + \frac 1{2n}$
. Then
$\alpha _* := \frac 12 + \frac 1{2n}$
. Then
 $$ \begin{align} \text{ if }n=2\text{ then } \sup_{\delta>0} \frac{\omega_\Omega(\delta)}{\delta^{\alpha_*}} &= \left( \frac{2^{3/2} }{\pi \sqrt{\kappa_0} }\right)^{1/2} \ , \end{align} $$
$$ \begin{align} \text{ if }n=2\text{ then } \sup_{\delta>0} \frac{\omega_\Omega(\delta)}{\delta^{\alpha_*}} &= \left( \frac{2^{3/2} }{\pi \sqrt{\kappa_0} }\right)^{1/2} \ , \end{align} $$
 $$ \begin{align} \text{ If }n\ge 3\text{ and }\partial\Omega\text{ is }C^2,\text{ then } \lim_{\delta \searrow 0} \frac{\omega_\Omega(\delta)}{\delta^{\alpha_*} } &= \left(\frac{2^{(n+1)/2}}{|B^n_1| \sqrt{\kappa_0}} \right)^{1/n}, \end{align} $$
$$ \begin{align} \text{ If }n\ge 3\text{ and }\partial\Omega\text{ is }C^2,\text{ then } \lim_{\delta \searrow 0} \frac{\omega_\Omega(\delta)}{\delta^{\alpha_*} } &= \left(\frac{2^{(n+1)/2}}{|B^n_1| \sqrt{\kappa_0}} \right)^{1/n}, \end{align} $$
where
![]() $|B^n_1|$
denotes the volume of the unit ball in
$|B^n_1|$
denotes the volume of the unit ball in
![]() $\mathbb {R}^n$
.
$\mathbb {R}^n$
.
Remark 1.2 The theorem implies that for
![]() $n=2$
,
$n=2$
,
 $$\begin{align*}[u]_{3/4} \le \left( \frac{2^{3/2} }{\pi \sqrt{\kappa_0} }\right)^{1/2} |\partial u(\Omega)|^{1/2} \qquad\text{ for all }u\in {C^\mathrm{con}_0}(\bar \Omega) \end{align*}$$
$$\begin{align*}[u]_{3/4} \le \left( \frac{2^{3/2} }{\pi \sqrt{\kappa_0} }\right)^{1/2} |\partial u(\Omega)|^{1/2} \qquad\text{ for all }u\in {C^\mathrm{con}_0}(\bar \Omega) \end{align*}$$
and that the estimate is sharp in the sense that it does not hold for any larger Hölder exponent or any smaller constant. Similarly, for
![]() $n\ge 3$
, since
$n\ge 3$
, since
![]() $\omega _\Omega (\delta )$
is continuous (this follows from (1.1) and the subadditivity of
$\omega _\Omega (\delta )$
is continuous (this follows from (1.1) and the subadditivity of
![]() $\omega _\Omega $
, which is easily deduced from the definition) and constant for
$\omega _\Omega $
, which is easily deduced from the definition) and constant for
![]() $\delta> \operatorname {diam}(\Omega )$
, the theorem implies that
$\delta> \operatorname {diam}(\Omega )$
, the theorem implies that
![]() $\sup _{\delta>0} \delta ^{-\alpha }\omega _\Omega (\delta ) <\infty $
, and hence that (1.5) holds, if and only if
$\sup _{\delta>0} \delta ^{-\alpha }\omega _\Omega (\delta ) <\infty $
, and hence that (1.5) holds, if and only if
![]() $\alpha \le \alpha _*$
.
$\alpha \le \alpha _*$
.
Note also that conclusion (1.8) may be described as an asymptotically sharp bound for the Hölder-
![]() $\alpha _*$
constant of
$\alpha _*$
constant of
![]() $u\in {C^\mathrm{con}_0}(\bar \Omega )$
on scales
$u\in {C^\mathrm{con}_0}(\bar \Omega )$
on scales
![]() $\le \delta $
, as
$\le \delta $
, as
![]() $\delta \to 0$
. It is natural to ask
$\delta \to 0$
. It is natural to ask
 $$\begin{align*}\text{for }n\ge 3,\text{ is it true that }\sup_{\delta>0}\frac{\omega_\Omega(\delta) }{ \delta^{\alpha_*}} = \left(\frac{2^{(n+1)/2}}{|B^n_1| \sqrt{\kappa_0}} \right)^{1/n} ? \end{align*}$$
$$\begin{align*}\text{for }n\ge 3,\text{ is it true that }\sup_{\delta>0}\frac{\omega_\Omega(\delta) }{ \delta^{\alpha_*}} = \left(\frac{2^{(n+1)/2}}{|B^n_1| \sqrt{\kappa_0}} \right)^{1/n} ? \end{align*}$$
This again would yield the sharp constant in (1.5) for the critical space. We are tempted to conjecture that the answer is “yes,” but we do not have any evidence to support this. We believe that the requirement that
![]() $\Omega $
is
$\Omega $
is
![]() $C^2$
is unnecessary and that convexity and (1.6) should suffice for (1.8).
$C^2$
is unnecessary and that convexity and (1.6) should suffice for (1.8).
Our other main result is less precise but completely general, in particular applying to domains for which the boundary curvature may vanish. As we will see, it implies that we can improve (1.1) to stronger Hölder norms as long as the domain satisfies a very weak nondegeneracy condition. It requires more notation. If
![]() $\Omega \subset \mathbb {R}^n$
is a convex set, we write
$\Omega \subset \mathbb {R}^n$
is a convex set, we write
![]() $\Omega ^\circ $
to denote the polar of
$\Omega ^\circ $
to denote the polar of
![]() $\Omega $
, defined by
$\Omega $
, defined by
For
![]() $a\in \Omega $
and
$a\in \Omega $
and
![]() $\nu \in S^{n-1}$
, we write
$\nu \in S^{n-1}$
, we write
 $$ \begin{align*} S(a,\nu)& := \{ x\in \mathbb{R}^n : x\cdot \nu = 0, \ \ a+x\in \Omega\} \\S^\circ(a,\nu) &:= \{ y\in \mathbb{R}^n : y\cdot \nu = 0, \ \ x\cdot y\le 1 \ \ \text{ for all }x\in S(a,\nu)\}\\&=\text{ polar of }S(a,\nu)\ \textit{within the hyperplane } \nu^\perp = \{ x\in \mathbb{R}^n : x\cdot\nu=0\}. \end{align*} $$
$$ \begin{align*} S(a,\nu)& := \{ x\in \mathbb{R}^n : x\cdot \nu = 0, \ \ a+x\in \Omega\} \\S^\circ(a,\nu) &:= \{ y\in \mathbb{R}^n : y\cdot \nu = 0, \ \ x\cdot y\le 1 \ \ \text{ for all }x\in S(a,\nu)\}\\&=\text{ polar of }S(a,\nu)\ \textit{within the hyperplane } \nu^\perp = \{ x\in \mathbb{R}^n : x\cdot\nu=0\}. \end{align*} $$
If
![]() $P\subset \mathbb {R}^n$
is a k-dimensional subspace and
$P\subset \mathbb {R}^n$
is a k-dimensional subspace and
![]() $A\subset P$
is a subset with relatively open interior, we will write
$A\subset P$
is a subset with relatively open interior, we will write
For example,
as long as
![]() $S^\circ (x,\nu )$
has open interior within
$S^\circ (x,\nu )$
has open interior within
![]() $\nu ^\perp $
, which will always be the case for us.
$\nu ^\perp $
, which will always be the case for us.
For
![]() $a\in \Omega $
, we will write
$a\in \Omega $
, we will write
and
 $$ \begin{align} N(a) = \left\{ \nu\in S^{n-1} : \exists y\in \partial \Omega \text{ such that }|a-y|=d_{\Omega}(a)\text{ and }\nu = \frac{y-a}{|y-a|} \right\} \end{align} $$
$$ \begin{align} N(a) = \left\{ \nu\in S^{n-1} : \exists y\in \partial \Omega \text{ such that }|a-y|=d_{\Omega}(a)\text{ and }\nu = \frac{y-a}{|y-a|} \right\} \end{align} $$
for the set of outer unit normals at boundary points closest to a.
We now state our second main result.
Theorem 1.3 Assume that
![]() $\Omega $
is a bounded, convex, and open subset of
$\Omega $
is a bounded, convex, and open subset of
![]() $\mathbb {R}^n$
. Then for every positive
$\mathbb {R}^n$
. Then for every positive
![]() $\delta \le \max _{a\in \Omega }d_{\Omega }(a)$
,
$\delta \le \max _{a\in \Omega }d_{\Omega }(a)$
,
 $$ \begin{align} \sup_{d_{\Omega}(a)=\delta} \ \sup_{\nu\in N(a)} \left( \frac{ \delta}{ 2|S^\circ(a, \nu)|}\right)^{1/n} \le \omega_\Omega(\delta) \le \sup_{d_{\Omega}(a)=\delta} \ \inf_{\nu\in N(a)} \left( \frac{ n\delta}{|S^\circ(a, \nu)|}\right)^{1/n}. \end{align} $$
$$ \begin{align} \sup_{d_{\Omega}(a)=\delta} \ \sup_{\nu\in N(a)} \left( \frac{ \delta}{ 2|S^\circ(a, \nu)|}\right)^{1/n} \le \omega_\Omega(\delta) \le \sup_{d_{\Omega}(a)=\delta} \ \inf_{\nu\in N(a)} \left( \frac{ n\delta}{|S^\circ(a, \nu)|}\right)^{1/n}. \end{align} $$
In principle, given a domain
![]() $\Omega $
with vanishing curvature, estimate (1.11) allows us to determine the exact scaling of
$\Omega $
with vanishing curvature, estimate (1.11) allows us to determine the exact scaling of
![]() $\omega _\Omega (\delta )$
as
$\omega _\Omega (\delta )$
as
![]() $\delta \searrow 0$
, and hence the exact range of exponents
$\delta \searrow 0$
, and hence the exact range of exponents
![]() $\alpha>1/n$
for which estimate (1.5) holds. We illustrate this in Section 3 below with several examples. For now, we note the following:
$\alpha>1/n$
for which estimate (1.5) holds. We illustrate this in Section 3 below with several examples. For now, we note the following:
Corollary 1.4 For
![]() $\Omega $
as above and
$\Omega $
as above and
![]() $\alpha>1/n$
, the Hölder-
$\alpha>1/n$
, the Hölder-
![]() $\alpha $
estimate (1.5) holds if and only if
$\alpha $
estimate (1.5) holds if and only if
for
![]() $\beta = n\alpha -1$
.
$\beta = n\alpha -1$
.
We omit the proof, as this follows directly from Theorem 1.3.
Remark 1.5 It is known that if
![]() $S\subset \mathbb {R}^n$
is any bounded convex set with nonempty interior, then
$S\subset \mathbb {R}^n$
is any bounded convex set with nonempty interior, then
see [Reference Kuperberg7] for a proof with a good estimate of
![]() $c_n$
(whose sharp value is the focus of the Mahler conjecture). Thus, (1.11) implies that there exists
$c_n$
(whose sharp value is the focus of the Mahler conjecture). Thus, (1.11) implies that there exists
![]() $C = C_n$
such that
$C = C_n$
such that
Remark 1.6 It is not hard to check that if
![]() $x\in \partial \Omega $
is a point at which
$x\in \partial \Omega $
is a point at which
![]() $\partial \Omega $
is twice differentiable, with Gaussian curvature
$\partial \Omega $
is twice differentiable, with Gaussian curvature
![]() $\kappa $
, and if
$\kappa $
, and if
![]() $\nu $
is the outer unit normal at x, then
$\nu $
is the outer unit normal at x, then
 $$ \begin{align} |S^\circ(x-\delta\nu, \nu)| = \frac{\sqrt \kappa |B^{n-1}_1|}{(2\delta)^{(n-1)/2}} (1+o(1)) \qquad\text{ as }\delta\to 0. \end{align} $$
$$ \begin{align} |S^\circ(x-\delta\nu, \nu)| = \frac{\sqrt \kappa |B^{n-1}_1|}{(2\delta)^{(n-1)/2}} (1+o(1)) \qquad\text{ as }\delta\to 0. \end{align} $$
We present the short proof in Lemma 3.4. This provides a quantitative link between the curvature at
![]() $x\in \partial \Omega $
and the rate of blowup of
$x\in \partial \Omega $
and the rate of blowup of
![]() $|S^\circ ( x-\delta \nu , \nu )|$
as
$|S^\circ ( x-\delta \nu , \nu )|$
as
![]() $\delta \searrow 0$
. In view of this, it is natural to interpret (1.12) as a degenerate positive curvature condition, growing more degenerate (and yielding a weaker Hölder exponent) as
$\delta \searrow 0$
. In view of this, it is natural to interpret (1.12) as a degenerate positive curvature condition, growing more degenerate (and yielding a weaker Hölder exponent) as
![]() $\beta $
decreases.
$\beta $
decreases.
To conclude this introduction, we note that several recent works have established sharp estimates of Hölder seminorms of solutions of Monge-Ampère equations of the form
for particular geometrically meaningful functions
![]() $F(x, u, Du)$
; see, for example, [Reference Chen and Jian1, Reference Jian and Li5, Reference Jian and Wang6, Reference Le8, Reference Le9]. Some of these papers allow for domains in which the boundary curvature can vanish, and they determine Hölder exponents that reflect the boundary behavior in a way that has some similarities to what we find in Theorem 1.3; see Corollary 3.1. The proofs in these references rely on careful constructions of sub- and supersolutions or. even in rare cases. explicit solutions. These play no role in our arguments.
$F(x, u, Du)$
; see, for example, [Reference Chen and Jian1, Reference Jian and Li5, Reference Jian and Wang6, Reference Le8, Reference Le9]. Some of these papers allow for domains in which the boundary curvature can vanish, and they determine Hölder exponents that reflect the boundary behavior in a way that has some similarities to what we find in Theorem 1.3; see Corollary 3.1. The proofs in these references rely on careful constructions of sub- and supersolutions or. even in rare cases. explicit solutions. These play no role in our arguments.
2 Preliminaries, and the proof of Theorem 1.3
Like all the results in this paper, those in this section are elementary, and many if not all (apart from the proof of Theorem 1.3, which. however, is an immediate corollary of other results) are presumably known to experts. For the convenience of the reader, we nonetheless provide complete proofs, mostly self-contained.
First, we recall some standard definitions. For
![]() $u\in {C^\mathrm{con}_0}(\bar \Omega )$
and
$u\in {C^\mathrm{con}_0}(\bar \Omega )$
and
![]() $x\in \Omega $
,
$x\in \Omega $
,
and for
![]() $A\subset \Omega $
,
$A\subset \Omega $
,
As mentioned above, if u is
![]() $C^2$
and strictly convex, then by the change of variables
$C^2$
and strictly convex, then by the change of variables
![]() $p = Du(x)$
,
$p = Du(x)$
,
(This remains true under somewhat weaker assumptions.) Given
![]() $a\in \Omega $
, we will write
$a\in \Omega $
, we will write
![]() $u_{a}:\bar \Omega \to \mathbb {R}$
to denote the function defined by
$u_{a}:\bar \Omega \to \mathbb {R}$
to denote the function defined by
The definition states that
and
![]() $u_a$
is linear on the line segment from any point on
$u_a$
is linear on the line segment from any point on
![]() $\partial \Omega $
to a. When we wish to explicitly indicate the dependence of
$\partial \Omega $
to a. When we wish to explicitly indicate the dependence of
![]() $u_a$
on
$u_a$
on
![]() $\Omega $
, we will write
$\Omega $
, we will write
![]() $u_{\Omega ,a}$
. It is well-known and straightforward to check that
$u_{\Omega ,a}$
. It is well-known and straightforward to check that
![]() $u_a$
is convex.
$u_a$
is convex.
Next, we define
![]() $f_\Omega :\Omega \to \mathbb {R}$
by
$f_\Omega :\Omega \to \mathbb {R}$
by
The following result implies that to understand the modulus of continuity for functions
![]() $u\in {C^\mathrm{con}_0}(\bar \Omega )$
with
$u\in {C^\mathrm{con}_0}(\bar \Omega )$
with
![]() $|\partial u(\Omega )|$
finite, it suffices to study the asymptotics of
$|\partial u(\Omega )|$
finite, it suffices to study the asymptotics of
![]() $f_\Omega (a)$
as
$f_\Omega (a)$
as
![]() $a\to \partial \Omega $
.
$a\to \partial \Omega $
.
Proposition 2.1 Let
![]() $\Omega $
be a bounded, convex, open subset of
$\Omega $
be a bounded, convex, open subset of
![]() $\mathbb {R}^n$
. Then the modulus
$\mathbb {R}^n$
. Then the modulus
![]() $\omega _\Omega $
defined in (1.3) satisfies
$\omega _\Omega $
defined in (1.3) satisfies
Proof
Step 1. We first claim that for
![]() $u\in {C^\mathrm{con}_0}(\bar \Omega )$
and any
$u\in {C^\mathrm{con}_0}(\bar \Omega )$
and any
![]() $a,b\in \Omega $
, there exists
$a,b\in \Omega $
, there exists
![]() $\bar a\in \Omega $
such that
$\bar a\in \Omega $
such that
We recall the proof, which is standard. Consider
![]() $a,b\in \Omega $
such that
$a,b\in \Omega $
such that
![]() $u(a) \le u(b)\le 0$
. Let
$u(a) \le u(b)\le 0$
. Let
![]() $\bar b$
be the point in
$\bar b$
be the point in
![]() $\partial \Omega $
on the ray that starts at a and passes through b. Then there exists some
$\partial \Omega $
on the ray that starts at a and passes through b. Then there exists some
![]() $\theta \in (0,1)$
such that
$\theta \in (0,1)$
such that
![]() $ b = (1-\theta )a + \theta \bar b$
. We next define
$ b = (1-\theta )a + \theta \bar b$
. We next define
![]() $\bar a = \theta a + (1-\theta ) \bar b$
. These definitions imply that
$\bar a = \theta a + (1-\theta ) \bar b$
. These definitions imply that
Thus,
![]() $d_{\Omega }(\bar a)\le |\bar a -\bar b| = |a-b|$
. Moreover, by convexity,
$d_{\Omega }(\bar a)\le |\bar a -\bar b| = |a-b|$
. Moreover, by convexity,
 $$ \begin{align*} u( b) - u(a) &= u((1-\theta)a + \theta \bar b) - u(a) \ \le \ \theta (u(\bar b) - u(a))\\ &= u(\bar b) - [ (1-\theta)u(\bar b) + \theta u(a)]\\ &\le u(\bar b) - u((1-\theta) \bar b + \theta a) \ = \ u(\bar b) - u(\bar a) = |u(\bar a)|. \end{align*} $$
$$ \begin{align*} u( b) - u(a) &= u((1-\theta)a + \theta \bar b) - u(a) \ \le \ \theta (u(\bar b) - u(a))\\ &= u(\bar b) - [ (1-\theta)u(\bar b) + \theta u(a)]\\ &\le u(\bar b) - u((1-\theta) \bar b + \theta a) \ = \ u(\bar b) - u(\bar a) = |u(\bar a)|. \end{align*} $$
Since
![]() $d_{\Omega }(\bar a)\le |a - b|$
, this proves (2.4).
$d_{\Omega }(\bar a)\le |a - b|$
, this proves (2.4).
Step 2. Given
![]() $u\in {C^\mathrm{con}_0}(\bar \Omega )$
,
$u\in {C^\mathrm{con}_0}(\bar \Omega )$
,
![]() $\delta>0$
and
$\delta>0$
and
![]() $x,y\in \Omega $
such that
$x,y\in \Omega $
such that
![]() $|x-y|\le \delta $
, fix
$|x-y|\le \delta $
, fix
![]() $a\in \Omega $
such that
$a\in \Omega $
such that
![]() $d_{\Omega }(a)\le \delta $
and
$d_{\Omega }(a)\le \delta $
and
![]() $|u(x)-u(y)|\le |u(a)|$
, and define
$|u(x)-u(y)|\le |u(a)|$
, and define
![]() $w(x) = u(a) u_a(x)$
. Then
$w(x) = u(a) u_a(x)$
. Then
![]() $u\le w\le 0$
in
$u\le w\le 0$
in
![]() $\Omega $
and
$\Omega $
and
![]() $u=w=0$
on
$u=w=0$
on
![]() $\partial \Omega $
, so standard arguments (see, for example, [Reference Gutiérrez4, Lemma 1.4.1]) imply that
$\partial \Omega $
, so standard arguments (see, for example, [Reference Gutiérrez4, Lemma 1.4.1]) imply that
with equality if and only if
![]() $u = w$
. The definition (1.3) of
$u = w$
. The definition (1.3) of
![]() $\omega _\Omega $
then implies that
$\omega _\Omega $
then implies that
Thus, for nonzero
![]() $u\in {C^\mathrm{con}_0}(\bar \Omega )$
,
$u\in {C^\mathrm{con}_0}(\bar \Omega )$
,
 $$\begin{align*}\text{ if }|x-y|\le \delta, \text{ then }\ \quad \ \frac{|u(x)-u(y)|}{ |\partial u(\Omega)|^{1/n} } \le \sup_{d_{\Omega}(a)\le \delta} f_\Omega(a)^{-1/n}. \end{align*}$$
$$\begin{align*}\text{ if }|x-y|\le \delta, \text{ then }\ \quad \ \frac{|u(x)-u(y)|}{ |\partial u(\Omega)|^{1/n} } \le \sup_{d_{\Omega}(a)\le \delta} f_\Omega(a)^{-1/n}. \end{align*}$$
It follows from this and the definition of
![]() $\omega _\Omega $
that
$\omega _\Omega $
that
However, given any
![]() $a\in \Omega $
such that
$a\in \Omega $
such that
![]() $d_{\Omega }(a)\le \delta $
, consider
$d_{\Omega }(a)\le \delta $
, consider
![]() $u = u_a$
, and fix
$u = u_a$
, and fix
![]() $b\in \partial \Omega $
such that
$b\in \partial \Omega $
such that
![]() $d_{\Omega }(a) = |a-b|$
. Then
$d_{\Omega }(a) = |a-b|$
. Then
 $$\begin{align*}|u_a(a)-u_a(b)| = |u_a(a)| = 1 = \frac {|\partial u_a(\Omega)|^{1/n}}{f_\Omega(a)^{1/n}}, \end{align*}$$
$$\begin{align*}|u_a(a)-u_a(b)| = |u_a(a)| = 1 = \frac {|\partial u_a(\Omega)|^{1/n}}{f_\Omega(a)^{1/n}}, \end{align*}$$
and thus,
 $$\begin{align*}\omega_\Omega(\delta) \ge \sup_{|x-y|\le \delta} \frac{|u_a(x)-u_a(y)|}{|\partial u_a(\Omega)|^{1/n}} \ge f_\Omega(a)^{-1/n} \qquad\text{ whenever }\ \ d_{\Omega}(a)\le \delta.\\[-43pt] \end{align*}$$
$$\begin{align*}\omega_\Omega(\delta) \ge \sup_{|x-y|\le \delta} \frac{|u_a(x)-u_a(y)|}{|\partial u_a(\Omega)|^{1/n}} \ge f_\Omega(a)^{-1/n} \qquad\text{ whenever }\ \ d_{\Omega}(a)\le \delta.\\[-43pt] \end{align*}$$
Motivated by Proposition 2.1, we record some properties of
![]() $f_\Omega $
and related notions.
$f_\Omega $
and related notions.
Lemma 2.1
![]() $\partial u_a(a) = \partial u_a(\Omega )$
.
$\partial u_a(a) = \partial u_a(\Omega )$
.
Proof It is clear that
![]() $\partial u_a(a) \subset \partial u_a(\Omega )$
. To prove the other inclusion, assume that
$\partial u_a(a) \subset \partial u_a(\Omega )$
. To prove the other inclusion, assume that
![]() $p\in \partial u(x_0)$
for some
$p\in \partial u(x_0)$
for some
![]() $x_0\in \Omega $
. We must show that
$x_0\in \Omega $
. We must show that
![]() $p\in \partial u(a)$
. We may assume that
$p\in \partial u(a)$
. We may assume that
![]() $x_0\ne a$
, so we can write
$x_0\ne a$
, so we can write
![]() $x_0 = \theta a + (1-\theta )y$
for some
$x_0 = \theta a + (1-\theta )y$
for some
![]() $y\in \partial \Omega $
and
$y\in \partial \Omega $
and
![]() $\theta \in (0,1)$
.
$\theta \in (0,1)$
.
For
![]() $x\in \Omega $
and
$x\in \Omega $
and
![]() $p\in \mathbb {R}^n$
, we will write
$p\in \mathbb {R}^n$
, we will write
![]() $\ell _{x,p}(z) := u_a(x) + p\cdot (z-x)$
, so that
$\ell _{x,p}(z) := u_a(x) + p\cdot (z-x)$
, so that
![]() $p\in \partial u_a(x)$
if and only if
$p\in \partial u_a(x)$
if and only if
![]() $\ell _{x,p}\le u_a$
in
$\ell _{x,p}\le u_a$
in
![]() $\Omega $
. Since
$\Omega $
. Since
![]() $u_a$
and
$u_a$
and
![]() $\ell _{x_0, p}$
are both linear when restricted to the segment
$\ell _{x_0, p}$
are both linear when restricted to the segment
![]() $\{ sa+(1-s)y : s\in (0,1]\}$
, and because
$\{ sa+(1-s)y : s\in (0,1]\}$
, and because
![]() $x_0$
belongs to the interior of this segment and
$x_0$
belongs to the interior of this segment and
![]() $u_a\ge \ell _{x_0,p}$
on this segment, we see that
$u_a\ge \ell _{x_0,p}$
on this segment, we see that
![]() $u_a = \ell _{x_0,p}$
on this segment, and in particular at
$u_a = \ell _{x_0,p}$
on this segment, and in particular at
![]() $x = a$
. Thus,
$x = a$
. Thus,
![]() $\ell _{x_0,p}$
is a supporting hyperplane at a; in fact,
$\ell _{x_0,p}$
is a supporting hyperplane at a; in fact,
![]() $\ell _{x_0,p} = \ell _{a,p}$
. It follows that
$\ell _{x_0,p} = \ell _{a,p}$
. It follows that
![]() $p\in \partial u_a(a)$
.
$p\in \partial u_a(a)$
.
Lemma 2.2 If
![]() $a \in \Omega \subset \Omega '$
, then
$a \in \Omega \subset \Omega '$
, then
![]() $f_{\Omega }(a) \ge f_{\Omega '}(a)$
.
$f_{\Omega }(a) \ge f_{\Omega '}(a)$
.
Proof If
![]() $p\in \partial u_{\Omega ',a}(\Omega ')$
, then
$p\in \partial u_{\Omega ',a}(\Omega ')$
, then
![]() $p\in \partial u_{\Omega ', a}(a)$
, which implies that
$p\in \partial u_{\Omega ', a}(a)$
, which implies that
![]() $\ell _{a,p}\le u_{\Omega ',a}$
in
$\ell _{a,p}\le u_{\Omega ',a}$
in
![]() $\Omega '$
. But it is easy to check that
$\Omega '$
. But it is easy to check that
![]() $u_{\Omega ',a} \le u_{\Omega ,a}$
in
$u_{\Omega ',a} \le u_{\Omega ,a}$
in
![]() $\Omega $
, and it follows that
$\Omega $
, and it follows that
![]() $\ell _{a,p}\le u_{\Omega ,a}$
in
$\ell _{a,p}\le u_{\Omega ,a}$
in
![]() $\Omega $
, which implies that
$\Omega $
, which implies that
![]() $p\in \partial u_{\Omega , a}(a)$
.
$p\in \partial u_{\Omega , a}(a)$
.
Thus,
![]() $\partial u_{\Omega ',a}(\Omega ') \subset \partial u_{\Omega ,a}(\Omega )$
, from which we deduce that
$\partial u_{\Omega ',a}(\Omega ') \subset \partial u_{\Omega ,a}(\Omega )$
, from which we deduce that
![]() $f_{\Omega '}(a)\le f_\Omega (a).$
$f_{\Omega '}(a)\le f_\Omega (a).$
Lemma 2.3 Assume that
![]() $\Omega \subset \mathbb {R}^n$
is bounded, convex, and open, with
$\Omega \subset \mathbb {R}^n$
is bounded, convex, and open, with
![]() $a\in \Omega $
.
$a\in \Omega $
.
Then
An equivalent statement appears as an exercise (problem 3.3) in the recent text [Reference Le10].
Proof We first prove the lemma for
![]() $a=0$
. We know from Lemma 2.1 that
$a=0$
. We know from Lemma 2.1 that
![]() $\partial u_0(\Omega ) = \partial u_0(0)$
. Then
$\partial u_0(\Omega ) = \partial u_0(0)$
. Then
 $$ \begin{align*} p\in \partial u_0(0) &\iff u_0(x) \ge u_0(0) + p\cdot x\text{ for all }x\in \Omega\\ &\iff u_0(x) \ge -1 + p\cdot x\text{ for all }x\in\bar \Omega. \end{align*} $$
$$ \begin{align*} p\in \partial u_0(0) &\iff u_0(x) \ge u_0(0) + p\cdot x\text{ for all }x\in \Omega\\ &\iff u_0(x) \ge -1 + p\cdot x\text{ for all }x\in\bar \Omega. \end{align*} $$
Since
![]() $u_0(x)\le 0$
in
$u_0(x)\le 0$
in
![]() $\Omega $
, it follows that
$\Omega $
, it follows that
However, if
![]() $p\in \Omega ^\circ $
, then
$p\in \Omega ^\circ $
, then
![]() $\ell _{0,p}(x):= -1+x\cdot p$
is an affine function such that
$\ell _{0,p}(x):= -1+x\cdot p$
is an affine function such that
![]() $\ell _{0,p} \le 0 = u_0$
on
$\ell _{0,p} \le 0 = u_0$
on
![]() $\partial \Omega $
and
$\partial \Omega $
and
![]() $\ell _{0,p}(0)=-1 = u_0(0)$
. It follows from this and the definition of
$\ell _{0,p}(0)=-1 = u_0(0)$
. It follows from this and the definition of
![]() $u_0$
that
$u_0$
that
![]() $\ell _{0,p} \le u_0$
in
$\ell _{0,p} \le u_0$
in
![]() $\Omega $
, and hence that
$\Omega $
, and hence that
![]() $p\in \partial u_0(0)$
.
$p\in \partial u_0(0)$
.
It follows that
![]() $\partial u_0(\Omega ) = \Omega ^\circ $
, and hence that
$\partial u_0(\Omega ) = \Omega ^\circ $
, and hence that
![]() $f_\Omega (0) = |\Omega ^\circ |$
.
$f_\Omega (0) = |\Omega ^\circ |$
.
For general
![]() $a\in \Omega $
, the definitions imply that for every
$a\in \Omega $
, the definitions imply that for every
![]() $x\in \Omega $
,
$x\in \Omega $
,
Thus,
![]() $f_\Omega (a) = |\partial u_{\Omega , a}( a) | = |\partial u_{\Omega -a,0}(0)| = |(\Omega -a)^\circ | $
.
$f_\Omega (a) = |\partial u_{\Omega , a}( a) | = |\partial u_{\Omega -a,0}(0)| = |(\Omega -a)^\circ | $
.
Lemma 2.4 Let
![]() $M:\mathbb {R}^n\to \mathbb {R}^n$
be an invertible linear transformation, and let
$M:\mathbb {R}^n\to \mathbb {R}^n$
be an invertible linear transformation, and let
![]() $M\Omega := \{ Mx: x\in \Omega \}$
. Then
$M\Omega := \{ Mx: x\in \Omega \}$
. Then
Proof The definitions imply that for every
![]() $x\in \Omega $
,
$x\in \Omega $
,
Thus, for every
![]() $x\in \Omega $
,
$x\in \Omega $
,
 $$ \begin{align*} &p\in \partial u_{M\Omega, Ma}(Mx) \\ &\qquad \ \ \Longleftrightarrow \ \ u_{M\Omega, Ma}(Mz) \ge u_{M\Omega, Ma}(Mx) + p \cdot (Mz-Mx)\qquad\text{ for all }Mz\in M\Omega\\ &\qquad \ \ \Longleftrightarrow \ \ u_{\Omega, a}(z) \ge u_{\Omega, a}(x) + M^Tp \cdot (z-x) \qquad\text{ for all }z\in \Omega. \\ &\qquad \ \ \Longleftrightarrow \ \ M^Tp\in \partial u_{\Omega,a}(x). \end{align*} $$
$$ \begin{align*} &p\in \partial u_{M\Omega, Ma}(Mx) \\ &\qquad \ \ \Longleftrightarrow \ \ u_{M\Omega, Ma}(Mz) \ge u_{M\Omega, Ma}(Mx) + p \cdot (Mz-Mx)\qquad\text{ for all }Mz\in M\Omega\\ &\qquad \ \ \Longleftrightarrow \ \ u_{\Omega, a}(z) \ge u_{\Omega, a}(x) + M^Tp \cdot (z-x) \qquad\text{ for all }z\in \Omega. \\ &\qquad \ \ \Longleftrightarrow \ \ M^Tp\in \partial u_{\Omega,a}(x). \end{align*} $$
We deduce that
![]() $\partial u_{M\Omega , Ma}(M\Omega ) = \{ M^{-T}p : p\in \partial u_{\Omega ,a}(\Omega )\}$
. Now the conclusion follows from basic properties of Lebesgue measure.
$\partial u_{M\Omega , Ma}(M\Omega ) = \{ M^{-T}p : p\in \partial u_{\Omega ,a}(\Omega )\}$
. Now the conclusion follows from basic properties of Lebesgue measure.
Lemma 2.5 Assume that
![]() $\Omega \subset \mathbb {R}^n$
is a bounded, open convex set containing the origin. For any subspace P of
$\Omega \subset \mathbb {R}^n$
is a bounded, open convex set containing the origin. For any subspace P of
![]() $\mathbb {R}^n$
, define
$\mathbb {R}^n$
, define
(Thus,
![]() $\Omega _P^\circ $
denotes the polar of
$\Omega _P^\circ $
denotes the polar of
![]() $\Omega _P$
within P rather than within the ambient
$\Omega _P$
within P rather than within the ambient
![]() $\mathbb {R}^n$
.)
$\mathbb {R}^n$
.)
Let
![]() $\pi _P:\mathbb {R}^n\to P$
denote orthogonal projection onto P.
$\pi _P:\mathbb {R}^n\to P$
denote orthogonal projection onto P.
Then
Proof We will show that
![]() $(\pi _P(\Omega ^\circ ))^\circ = (\Omega _P^\circ )^\circ = \bar \Omega _P$
, where our convention is that if
$(\pi _P(\Omega ^\circ ))^\circ = (\Omega _P^\circ )^\circ = \bar \Omega _P$
, where our convention is that if
![]() $A\subset P$
is convex, then
$A\subset P$
is convex, then
![]() $A^\circ $
denotes the polar within P, whereas if A is a convex set not contained in P, then
$A^\circ $
denotes the polar within P, whereas if A is a convex set not contained in P, then
![]() $A^\circ $
denotes its polar in
$A^\circ $
denotes its polar in
![]() $\mathbb {R}^n$
. Then
$\mathbb {R}^n$
. Then
 $$ \begin{align*} y\in (\pi_P(\Omega^\circ))^\circ &\ \ \Longleftrightarrow \ \ y\in P\text{ and }y\cdot x\le 1\quad\text{ for all }x\in \pi_P(\Omega^\circ)\\ &\ \ \Longleftrightarrow \ \ y\in P\text{ and } y\cdot \pi_P x\le 1\quad\text{ for all }x\in \Omega^\circ\\ &\ \ \Longleftrightarrow \ \ y\in P\text{ and } y\cdot x\le 1\quad\text{ for all }x\in \Omega^\circ\\ &\ \ \Longleftrightarrow \ \ y\in P \cap (\Omega^\circ)^\circ = P\cap \bar \Omega = \bar \Omega_P, \end{align*} $$
$$ \begin{align*} y\in (\pi_P(\Omega^\circ))^\circ &\ \ \Longleftrightarrow \ \ y\in P\text{ and }y\cdot x\le 1\quad\text{ for all }x\in \pi_P(\Omega^\circ)\\ &\ \ \Longleftrightarrow \ \ y\in P\text{ and } y\cdot \pi_P x\le 1\quad\text{ for all }x\in \Omega^\circ\\ &\ \ \Longleftrightarrow \ \ y\in P\text{ and } y\cdot x\le 1\quad\text{ for all }x\in \Omega^\circ\\ &\ \ \Longleftrightarrow \ \ y\in P \cap (\Omega^\circ)^\circ = P\cap \bar \Omega = \bar \Omega_P, \end{align*} $$
completing the proof.
Lemma 2.6 Let
![]() $\Omega $
be an open convex subset of
$\Omega $
be an open convex subset of
![]() $\mathbb {R}^n$
with nonempty boundary. For
$\mathbb {R}^n$
with nonempty boundary. For
![]() $a\in \Omega $
, let
$a\in \Omega $
, let
![]() $x\in \partial \Omega $
be a point such that
$x\in \partial \Omega $
be a point such that
![]() $|a-x| = d_{\Omega }(a)$
, and let
$|a-x| = d_{\Omega }(a)$
, and let
![]() $\nu = \frac {x-a}{|x-a|}$
. (Thus,
$\nu = \frac {x-a}{|x-a|}$
. (Thus,
![]() $\nu \in N(a)$
, in the notation introduced in (1.10).) Then
$\nu \in N(a)$
, in the notation introduced in (1.10).) Then
Remark 2.7 A curious consequence of (2.7) is that for
![]() $a\in \Omega $
, if there exist more than one point
$a\in \Omega $
, if there exist more than one point
![]() $b\in \partial \Omega $
such that
$b\in \partial \Omega $
such that
![]() $d_{\Omega }(a) = |b-a|$
, then
$d_{\Omega }(a) = |b-a|$
, then
Proof
Step 1. After a translation and a rotation, we may assume that
![]() $a=0$
and that
$a=0$
and that
![]() $x = (0,\ldots , 0,-\delta )$
, where
$x = (0,\ldots , 0,-\delta )$
, where
![]() $\delta = d_{\Omega }(a)$
. Then
$\delta = d_{\Omega }(a)$
. Then
![]() $-e_n$
is the outer unit normal at x, and hence,
$-e_n$
is the outer unit normal at x, and hence,
![]() $\Omega \subset \{ y\in \mathbb {R}^n : y_n> -\delta \}$
. One can then quickly check that
$\Omega \subset \{ y\in \mathbb {R}^n : y_n> -\delta \}$
. One can then quickly check that
Let
![]() $P := \mathbb {R}^{n-1}\times \{0\}$
, so that
$P := \mathbb {R}^{n-1}\times \{0\}$
, so that
![]() $\Omega _P = S(a,\nu )$
. It then follows from Lemma 2.5 that
$\Omega _P = S(a,\nu )$
. It then follows from Lemma 2.5 that
Now let T denote the Steiner symmetrization of
![]() $\Omega ^\circ $
with respect to the hyperplane
$\Omega ^\circ $
with respect to the hyperplane
![]() $x_n=0$
. Well-known properties of Steiner symmetrization imply that
$x_n=0$
. Well-known properties of Steiner symmetrization imply that
![]() $|T| = |\Omega ^\circ |$
, that T inherits the convexity of
$|T| = |\Omega ^\circ |$
, that T inherits the convexity of
![]() $\Omega ^\circ $
, and, owing to (2.8), (2.9), that
$\Omega ^\circ $
, and, owing to (2.8), (2.9), that
By convexity, T contains the cones in
![]() $\mathbb {R}^n$
with base
$\mathbb {R}^n$
with base
![]() $S^\circ (a,\nu )\subset \mathbb {R}^{n-1}\times \{0\}$
with vertices at
$S^\circ (a,\nu )\subset \mathbb {R}^{n-1}\times \{0\}$
with vertices at
![]() $\pm \frac 1 {2\delta }e_n$
. Each of these cones has measure
$\pm \frac 1 {2\delta }e_n$
. Each of these cones has measure
![]() $\frac 1{2 \delta n} |S^\circ (a,\nu )|$
. We conclude that
$\frac 1{2 \delta n} |S^\circ (a,\nu )|$
. We conclude that
Step 2. Let
![]() $P^\perp = \{0^{n-1}\}\times \mathbb {R}$
, the orthogonal complement of P. Since
$P^\perp = \{0^{n-1}\}\times \mathbb {R}$
, the orthogonal complement of P. Since
![]() $a=0$
and
$a=0$
and
![]() $d_{\Omega }(a) \ge \delta $
, it is clear that
$d_{\Omega }(a) \ge \delta $
, it is clear that
![]() $\Omega \cap P^\perp = \Omega _{P^\perp } \supset \{0^{n-1}\}\times (-\delta ,\delta )$
. It easily follows that
$\Omega \cap P^\perp = \Omega _{P^\perp } \supset \{0^{n-1}\}\times (-\delta ,\delta )$
. It easily follows that
![]() $\Omega _{P^\perp }^\circ \subset \{0^{n-1}\}\times (-\frac 1\delta , \frac 1\delta )$
. In addition, Lemma 2.6 implies that
$\Omega _{P^\perp }^\circ \subset \{0^{n-1}\}\times (-\frac 1\delta , \frac 1\delta )$
. In addition, Lemma 2.6 implies that
It follows from these facts and (2.9) that
(writing
![]() $S^0(a,\nu )$
as a subset of
$S^0(a,\nu )$
as a subset of
![]() $\mathbb {R}^{n-1}$
rather than of
$\mathbb {R}^{n-1}$
rather than of
![]() $\mathbb {R}^{n-1}\times \{0\}$
). Thus,
$\mathbb {R}^{n-1}\times \{0\}$
). Thus,
3 Examples
Our first illustration of the utility of Theorem 1.3 addresses a class of convex sets considered in several recent papers.
Corollary 3.1 Let
![]() $\Omega $
be a bounded, open convex subset of
$\Omega $
be a bounded, open convex subset of
![]() $\mathbb {R}^n$
, and assume that there exist positive constants
$\mathbb {R}^n$
, and assume that there exist positive constants
![]() $\eta $
and
$\eta $
and
![]() $p_1,\dots , p_k$
, with
$p_1,\dots , p_k$
, with
![]() $k\le n-1$
, such that at any
$k\le n-1$
, such that at any
![]() $b\in \partial \Omega $
, after a translation and a rotation,
$b\in \partial \Omega $
, after a translation and a rotation,
Then there exists a constant C, depending on
![]() $\eta , n, \operatorname {diam}(\Omega )$
, such that
$\eta , n, \operatorname {diam}(\Omega )$
, such that
 $$\begin{align*}[u]_\alpha \le C|\partial u(\Omega)|^{1/n} \ \ \ \text{ for all }u\in {C^\mathrm{con}_0}(\bar \Omega), \qquad\text{ where }\alpha = \frac 1n(1 + \sum_{j=1}^k \frac 1{p_j}). \end{align*}$$
$$\begin{align*}[u]_\alpha \le C|\partial u(\Omega)|^{1/n} \ \ \ \text{ for all }u\in {C^\mathrm{con}_0}(\bar \Omega), \qquad\text{ where }\alpha = \frac 1n(1 + \sum_{j=1}^k \frac 1{p_j}). \end{align*}$$
Note that (3.1) allows
![]() $\Omega $
to be completely degenerate at b in
$\Omega $
to be completely degenerate at b in
![]() $n-k-1$
directions.
$n-k-1$
directions.
In [Reference Chen and Jian1, Reference Jian and Wang6], sharp Hölder estimates on domains satisfying (3.1) at every
![]() $b\in \partial \Omega $
(for a suitable b-dependent choice of coordinates) are proved for solutions of certain equations of the form (1.16). Interestingly, the quantity
$b\in \partial \Omega $
(for a suitable b-dependent choice of coordinates) are proved for solutions of certain equations of the form (1.16). Interestingly, the quantity
![]() $\sum _{j=1}^k \frac 1{p_j}$
also appears in the Hölder exponents in these results, modified by other parameters appearing in the nonlinearity on the right-hand side of (1.16).
$\sum _{j=1}^k \frac 1{p_j}$
also appears in the Hölder exponents in these results, modified by other parameters appearing in the nonlinearity on the right-hand side of (1.16).
Proof Let
![]() $\delta>0$
and
$\delta>0$
and
![]() $a\in \Omega $
with
$a\in \Omega $
with
![]() $d_{\Omega }(a)=|a-b|=\delta $
for some
$d_{\Omega }(a)=|a-b|=\delta $
for some
![]() $b\in \partial \Omega $
. After a translation and rotation, we may assume that (3.1) holds. We necessarily have that
$b\in \partial \Omega $
. After a translation and rotation, we may assume that (3.1) holds. We necessarily have that
![]() $a=(0, \ldots , 0, \delta )$
. Indeed, suppose
$a=(0, \ldots , 0, \delta )$
. Indeed, suppose
![]() $a_i\ne 0$
for some
$a_i\ne 0$
for some
![]() $1\le i \le n-1$
. Then from the supporting hyperplane
$1\le i \le n-1$
. Then from the supporting hyperplane
![]() $\{x_{n}=0\}$
, we obtain
$\{x_{n}=0\}$
, we obtain
a contradiction, verifying the claim.
Now, relabeling coordinates, we write the unit outer normal at b as
![]() $\nu =-e_{n}$
and have that
$\nu =-e_{n}$
and have that
 $$ \begin{align*} S(a,\nu) &\subseteq \left\{x\in \mathbb{R}^{n-1}\times \{0\}: \delta> \eta \sum_{i=1}^k |x_i|^{p_i}, \ \ |(x_{k+1}, \ldots x_{n-1})|< \text{diam}(\Omega)\right\}. \end{align*} $$
$$ \begin{align*} S(a,\nu) &\subseteq \left\{x\in \mathbb{R}^{n-1}\times \{0\}: \delta> \eta \sum_{i=1}^k |x_i|^{p_i}, \ \ |(x_{k+1}, \ldots x_{n-1})|< \text{diam}(\Omega)\right\}. \end{align*} $$
Thus,
![]() $|S(a,\nu )|$
is bounded by the volume of the set on the right, which is
$|S(a,\nu )|$
is bounded by the volume of the set on the right, which is
for a constant C dependingFootnote
1
on
![]() $\eta , p_1,\ldots , p_k, k, n-1, \text {diam}(\Omega )$
. Since a was arbitrary, (1.13) and Theorem 1.3 (or see (1.14)) imply that
$\eta , p_1,\ldots , p_k, k, n-1, \text {diam}(\Omega )$
. Since a was arbitrary, (1.13) and Theorem 1.3 (or see (1.14)) imply that
Hence, the result on the Hölder estimate.
If there is any point
![]() $b\in \partial \Omega $
such that after a translation and a rotation
$b\in \partial \Omega $
such that after a translation and a rotation
for some positive numbers
![]() $\eta , p_1,\ldots , p_k, h$
, then by a similar argument to that above, one can show that
$\eta , p_1,\ldots , p_k, h$
, then by a similar argument to that above, one can show that
![]() $\omega _\Omega (\delta ) \ge c \delta ^\alpha $
for all sufficiently small
$\omega _\Omega (\delta ) \ge c \delta ^\alpha $
for all sufficiently small
![]() $\delta $
and the same
$\delta $
and the same
![]() $\alpha $
as above. This would use the fact that if S is a centrally symmetric convex body in
$\alpha $
as above. This would use the fact that if S is a centrally symmetric convex body in
![]() $\mathbb {R}^k$
, then
$\mathbb {R}^k$
, then
![]() $|S| \, |S^\circ | \le |B^k_1|^2$
.
$|S| \, |S^\circ | \le |B^k_1|^2$
.
The following lemma provides a way to generate a large class of examples.
Lemma 3.2 Assume that
![]() $\Omega \subset \mathbb {R}^2$
is a smooth convex set of the form
$\Omega \subset \mathbb {R}^2$
is a smooth convex set of the form
for some
![]() $R, D>0$
, where
$R, D>0$
, where
![]() $h:[-R,R]\to [0,\infty )$
is an even function, smooth on
$h:[-R,R]\to [0,\infty )$
is an even function, smooth on
![]() $(-R,R)$
, such that
$(-R,R)$
, such that
![]() $h(0)=h'(0) = h"(0)=0$
and
$h(0)=h'(0) = h"(0)=0$
and
![]() $h(R) = \frac D2$
.
$h(R) = \frac D2$
.
Assume, moreover, that the boundary curvature is nondecreasing as one moves in the direction of increasing
![]() $x_1$
along
$x_1$
along
![]() $\partial \Omega $
from
$\partial \Omega $
from
![]() $(0, 0)$
toward
$(0, 0)$
toward
![]() $(R,D/2)$
.
$(R,D/2)$
.
Then, writing
![]() $h^{-1}(\delta )$
to denote the unique positive solution of the equation
$h^{-1}(\delta )$
to denote the unique positive solution of the equation
![]() $h(x)=\delta $
for
$h(x)=\delta $
for
![]() $0<\delta \le D/2$
, there exists
$0<\delta \le D/2$
, there exists
![]() $\delta _0>0$
such that
$\delta _0>0$
such that
The lemma implies that given any modulus of the form
![]() $\omega (\delta ) = \sqrt {\delta h^{-1}(\delta )}$
for h satisfying the above hypotheses, we can construct a domain for which the sharp modulus of continuity
$\omega (\delta ) = \sqrt {\delta h^{-1}(\delta )}$
for h satisfying the above hypotheses, we can construct a domain for which the sharp modulus of continuity
![]() $\omega _\Omega $
in the Alexandrov estimate exactly agrees with
$\omega _\Omega $
in the Alexandrov estimate exactly agrees with
![]() $\omega $
, up to a factor of
$\omega $
, up to a factor of
![]() $2\sqrt 2$
.
$2\sqrt 2$
.
Proof Assume that
![]() $0<\delta <\delta _0$
, to be fixed below.
$0<\delta <\delta _0$
, to be fixed below.
Step 1. It is clear from (3.2) and properties of h that if
![]() $\delta _0$
is sufficiently small (in fact, here,
$\delta _0$
is sufficiently small (in fact, here,
![]() $\delta _0<D/2$
is sufficient), then the origin is the unique closest boundary point to
$\delta _0<D/2$
is sufficient), then the origin is the unique closest boundary point to
![]() $(0,\delta )$
, and hence that
$(0,\delta )$
, and hence that
![]() $N(a)$
as defined in (1.10) consists of
$N(a)$
as defined in (1.10) consists of
![]() $\{ -e_2\}$
. Then the definitions imply that
$\{ -e_2\}$
. Then the definitions imply that
Recall our convention that
![]() $S^\circ (a,\nu )$
denotes the polar within the subspace
$S^\circ (a,\nu )$
denotes the polar within the subspace
![]() $\nu ^\perp $
. If a and b are positive numbers, then
$\nu ^\perp $
. If a and b are positive numbers, then
![]() $(a,b)^\circ = [\frac 1a, \frac 1b]$
, so it follows that
$(a,b)^\circ = [\frac 1a, \frac 1b]$
, so it follows that
This and Theorem 1.3 imply the lower bound for
![]() $\omega _\Omega (\delta )$
in (3.3).
$\omega _\Omega (\delta )$
in (3.3).
Step 2. To complete the proof of the Lemma, again by Theorem 1.3, it suffices to show that if
![]() $d_{\Omega }(a)=\delta $
and
$d_{\Omega }(a)=\delta $
and
![]() $\nu \in N(a)$
, then
$\nu \in N(a)$
, then
if
![]() $\delta _0$
is small enough. Fix any
$\delta _0$
is small enough. Fix any
![]() $a\in \Omega $
such that
$a\in \Omega $
such that
![]() $d_{\Omega }(a)=\delta $
and any
$d_{\Omega }(a)=\delta $
and any
![]() $b\in \partial \Omega $
such that
$b\in \partial \Omega $
such that
![]() $d_{\Omega }(a)=|a-b|$
, and let
$d_{\Omega }(a)=|a-b|$
, and let
![]() $\nu = \frac {b-a}{|b-a|}$
. Noting from (3.2) that
$\nu = \frac {b-a}{|b-a|}$
. Noting from (3.2) that
![]() $\Omega $
is symmetric about the
$\Omega $
is symmetric about the
![]() $x_2$
axis (since h is even) and about the line
$x_2$
axis (since h is even) and about the line
![]() $x_2 = D/2$
, we can assume that
$x_2 = D/2$
, we can assume that
![]() $b\in \{(x_1, x_2)\in \partial \Omega : 0\le x_1\le R, x_2 = h(x_1)\}$
.
$b\in \{(x_1, x_2)\in \partial \Omega : 0\le x_1\le R, x_2 = h(x_1)\}$
.
Then we define
![]() $\widetilde \Omega $
to be the set obtained by translating b to the origin and rotating so that
$\widetilde \Omega $
to be the set obtained by translating b to the origin and rotating so that
![]() $\widetilde \Omega \subset \{(x_1, x_2): x_2>0\}$
. This operation moves a to the point
$\widetilde \Omega \subset \{(x_1, x_2): x_2>0\}$
. This operation moves a to the point
![]() $(0,\delta )$
. Next, we let
$(0,\delta )$
. Next, we let
![]() $\tilde h_1$
be the function whose graph parametrizes the lower part of
$\tilde h_1$
be the function whose graph parametrizes the lower part of
![]() $\partial \widetilde \Omega $
, defined by
$\partial \widetilde \Omega $
, defined by
![]() $\tilde h(x_1) := \inf \{ x_2\in \mathbb {R} : (x_1, x_2)\in \widetilde \Omega \}$
. By our assumption about the monotonicity of the boundary curvature along the short arc connecting
$\tilde h(x_1) := \inf \{ x_2\in \mathbb {R} : (x_1, x_2)\in \widetilde \Omega \}$
. By our assumption about the monotonicity of the boundary curvature along the short arc connecting
![]() $(0,0)$
to
$(0,0)$
to
![]() $(R,D/2)$
, we see that if
$(R,D/2)$
, we see that if
![]() $\delta _0$
is small enough, then
$\delta _0$
is small enough, then
for
![]() $0< x_1 < h^{-1}(\delta _0)$
. Since
$0< x_1 < h^{-1}(\delta _0)$
. Since
![]() $\tilde h(0) = \tilde h'(0) = h(0) = h'(0)$
, and because
$\tilde h(0) = \tilde h'(0) = h(0) = h'(0)$
, and because
![]() $0=h"(0)\le \tilde h"(0)$
, this implies that
$0=h"(0)\le \tilde h"(0)$
, this implies that
![]() $\tilde h(x_1) \ge h(x_1)$
for
$\tilde h(x_1) \ge h(x_1)$
for
![]() $0<x_1< h^{-1}(\delta _0)$
.
$0<x_1< h^{-1}(\delta _0)$
.
Computing
![]() $S^\circ (a,\nu )$
in the coordinate system of
$S^\circ (a,\nu )$
in the coordinate system of
![]() $\widetilde \Omega $
, we find that
$\widetilde \Omega $
, we find that
![]() $S(a,\nu ) = (-\alpha , \beta )\times \{0\}$
, where
$S(a,\nu ) = (-\alpha , \beta )\times \{0\}$
, where
![]() $-\alpha ,\beta $
are the negative and positive solutions, respectively, of the equation
$-\alpha ,\beta $
are the negative and positive solutions, respectively, of the equation
![]() $\tilde h(x)=\delta $
, and thus,
$\tilde h(x)=\delta $
, and thus,
But the fact that
![]() $\tilde h \ge h$
for
$\tilde h \ge h$
for
![]() $0<x_1< h^{-1}(\delta _0)$
implies that
$0<x_1< h^{-1}(\delta _0)$
implies that
![]() $\beta \le h^{-1}(\delta )$
, proving (3.4).
$\beta \le h^{-1}(\delta )$
, proving (3.4).
Based on the above lemma, it is straightforward to construct examples of domains
![]() $\Omega \subset \mathbb {R}^2$
such that
$\Omega \subset \mathbb {R}^2$
such that
![]() $\omega _\Omega (\delta ) \sim \delta ^{1/p}$
for given
$\omega _\Omega (\delta ) \sim \delta ^{1/p}$
for given
![]() $p>2$
. Another example is obtained by taking
$p>2$
. Another example is obtained by taking
![]() $h(x)$
in (3.2) such that
$h(x)$
in (3.2) such that
and extended (after choosing a small enough) so that the graph of h has increasing curvature until the point where its tangent becomes vertical. Then the lemma implies that for the resulting domain
![]() $\Omega $
,
$\Omega $
,
 $$\begin{align*}\frac 12 \left( \frac{\delta}{|\log \delta|} \right)^{1/2} \le \omega_\Omega(\delta) \le \sqrt 2 \left( \frac{\delta}{|\log \delta|} \right)^{1/2}. \end{align*}$$
$$\begin{align*}\frac 12 \left( \frac{\delta}{|\log \delta|} \right)^{1/2} \le \omega_\Omega(\delta) \le \sqrt 2 \left( \frac{\delta}{|\log \delta|} \right)^{1/2}. \end{align*}$$
In this spirit, it would be straightforward to construct sets with
![]() $\omega _\Omega $
, for example, having logarithmic or other corrections to Hölder moduli
$\omega _\Omega $
, for example, having logarithmic or other corrections to Hölder moduli
![]() $\delta ^\alpha $
for some
$\delta ^\alpha $
for some
![]() $\frac 1n <\alpha < \frac 12 + \frac 1{2n}$
.
$\frac 1n <\alpha < \frac 12 + \frac 1{2n}$
.
The next lemma shows that, loosely speaking, the scaling in the classical Alexandrov estimate (1.1) is almost never optimal:
Lemma 3.3 Let
![]() $\Omega \subset \mathbb {R}^n$
be a convex, open domain, and assume that
$\Omega \subset \mathbb {R}^n$
be a convex, open domain, and assume that
![]() $\Omega \subset B_R$
for some
$\Omega \subset B_R$
for some
![]() $R>0$
. Then
$R>0$
. Then
In fact, if
![]() $\omega _\Omega (\delta ) \ge A\delta ^{1/n}$
for
$\omega _\Omega (\delta ) \ge A\delta ^{1/n}$
for
![]() $\delta \in (0,\delta _0)$
, then there exists a supporting hyperplane P such that
$\delta \in (0,\delta _0)$
, then there exists a supporting hyperplane P such that
The estimate of the radius of the ball is not sharp.
Proof We first claim that for
![]() $R, c>0$
and
$R, c>0$
and
![]() $S\subset \mathbb {R}^k$
,
$S\subset \mathbb {R}^k$
,
 $$ \begin{align} \text{ if }S\subset B_R \text{ and }|S^\circ|<c, \qquad\text{ then } B_r\subset S \text{ for }r= \frac {|B^{k-1}_1|}{2c(2R)^{k-1}}. \end{align} $$
$$ \begin{align} \text{ if }S\subset B_R \text{ and }|S^\circ|<c, \qquad\text{ then } B_r\subset S \text{ for }r= \frac {|B^{k-1}_1|}{2c(2R)^{k-1}}. \end{align} $$
Indeed, for
![]() $r<R$
, suppose
$r<R$
, suppose
![]() $S\subset B_R$
does not contain
$S\subset B_R$
does not contain
![]() $B_r$
. By a rotation, we may assume that there is a point of the form
$B_r$
. By a rotation, we may assume that there is a point of the form
![]() $b = (0,\ldots , 0, r_1)$
with
$b = (0,\ldots , 0, r_1)$
with
![]() $0<r_1<r$
such that
$0<r_1<r$
such that
![]() $d_S(0) = |0 - b| = r_1$
. Then the plane
$d_S(0) = |0 - b| = r_1$
. Then the plane
![]() $\{ x : x_k = r_1\}$
is a supporting hyperplane at b, so
$\{ x : x_k = r_1\}$
is a supporting hyperplane at b, so
![]() $S\subset B_R \cap \{ x : x_k < r_1\}$
. We claim that
$S\subset B_R \cap \{ x : x_k < r_1\}$
. We claim that
This is clear, since if
![]() $y = (y', y_n)$
belongs to the set on the left, then one readily checks that
$y = (y', y_n)$
belongs to the set on the left, then one readily checks that
![]() $x\cdot y\le 1$
for all
$x\cdot y\le 1$
for all
![]() $x\in S \subset B_R \cap \{ x : x_k<r_1\}$
, proving (3.6). It follows that
$x\in S \subset B_R \cap \{ x : x_k<r_1\}$
, proving (3.6). It follows that
 $$\begin{align*}c> |S^\circ| \ge \frac {|B^{k-1}_1|}{2r_1(2R)^{k-1} } \ge \frac {|B^{k-1}_1|}{2r(2R)^{k-1}}. \end{align*}$$
$$\begin{align*}c> |S^\circ| \ge \frac {|B^{k-1}_1|}{2r_1(2R)^{k-1} } \ge \frac {|B^{k-1}_1|}{2r(2R)^{k-1}}. \end{align*}$$
This cannot happen if
![]() $r \le \frac {|B^{k-1}_1|}{2c(2R)^{k-1}}$
. So for such r, it must be the case that
$r \le \frac {|B^{k-1}_1|}{2c(2R)^{k-1}}$
. So for such r, it must be the case that
![]() $B_r\subset S$
, proving (3.5).
$B_r\subset S$
, proving (3.5).
Now assume that there exists
![]() $A>0$
such that
$A>0$
such that
![]() $\omega _\Omega (\delta )\ge A \delta ^{1/n}$
, and fix a sequence
$\omega _\Omega (\delta )\ge A \delta ^{1/n}$
, and fix a sequence
![]() $a_j\in \Omega $
and
$a_j\in \Omega $
and
![]() $\nu _j\in N(a_j)$
such that
$\nu _j\in N(a_j)$
such that
![]() $d_{\Omega }(a_j) := \delta _j\to 0$
, and
$d_{\Omega }(a_j) := \delta _j\to 0$
, and
![]() $|S^\circ (a_j, \nu _j)| < n A^{-n}$
. The existence of such sequences follows directly from Theorem 1.3. Upon passing to subsequences (still labeled
$|S^\circ (a_j, \nu _j)| < n A^{-n}$
. The existence of such sequences follows directly from Theorem 1.3. Upon passing to subsequences (still labeled
![]() $a_j, \nu _j, \delta _j$
) we may assume that
$a_j, \nu _j, \delta _j$
) we may assume that
![]() $a_j\to b\in \partial \Omega $
. After a translation and a rotation, we may assume that
$a_j\to b\in \partial \Omega $
. After a translation and a rotation, we may assume that
![]() $b=0$
and
$b=0$
and
![]() $\Omega \subset \{ x\in \mathbb {R}^n : x_n>0\}$
.
$\Omega \subset \{ x\in \mathbb {R}^n : x_n>0\}$
.
Appealing to (3.5) with
![]() $k=n-1$
, we find that
$k=n-1$
, we find that
![]() $B_r\subset S(a_j, \nu _j)$
with
$B_r\subset S(a_j, \nu _j)$
with
![]() $r = \frac {|B^{n-2}_1| A^n }{2^{n-1}n R^{n-2}}$
. Then the definition of
$r = \frac {|B^{n-2}_1| A^n }{2^{n-1}n R^{n-2}}$
. Then the definition of
![]() $S(a_j,\nu _j)$
implies that
$S(a_j,\nu _j)$
implies that
This implies that
![]() $\nu _j\to - e_n $
as
$\nu _j\to - e_n $
as
![]() $j\to \infty $
and
$j\to \infty $
and
![]() $a_j\to b=0$
. Then
$a_j\to b=0$
. Then
as
![]() $j\to \infty $
, in the Hausdorff distance. It follows that
$j\to \infty $
, in the Hausdorff distance. It follows that
![]() $B^{n-1}_r\times \{0\}\subset \bar \Omega $
, and hence, since
$B^{n-1}_r\times \{0\}\subset \bar \Omega $
, and hence, since
![]() $\Omega \subset \{x : x_n>0\}$
, we conclude that
$\Omega \subset \{x : x_n>0\}$
, we conclude that
![]() $B^{n-1}_r\times \{0\}\subset \partial \Omega $
. Thus, we have found a flat spot.
$B^{n-1}_r\times \{0\}\subset \partial \Omega $
. Thus, we have found a flat spot.
We omit the proof that if
![]() $\partial \Omega $
has a flat spot, then
$\partial \Omega $
has a flat spot, then
![]() $\omega _\Omega (\delta ) \ge c\delta ^{1/n}$
for some c, which is a very direct consequence of Theorem 1.3.
$\omega _\Omega (\delta ) \ge c\delta ^{1/n}$
for some c, which is a very direct consequence of Theorem 1.3.
Finally, we present the proof of a fact already stated in the introduction.
Lemma 3.4 If
![]() $x\in \partial \Omega $
is a point at which
$x\in \partial \Omega $
is a point at which
![]() $\partial \Omega $
is twice differentiable, with Gaussian curvature
$\partial \Omega $
is twice differentiable, with Gaussian curvature
![]() $\kappa $
, and if
$\kappa $
, and if
![]() $\nu $
is the outer unit normal at x, then
$\nu $
is the outer unit normal at x, then
 $$ \begin{align} |S^\circ(x-\delta\nu, \nu)| = \frac{\sqrt \kappa |B^{n-1}_1|}{(2\delta)^{(n-1)/2}} (1+o(1)) \qquad\text{ as }\delta\to 0. \end{align} $$
$$ \begin{align} |S^\circ(x-\delta\nu, \nu)| = \frac{\sqrt \kappa |B^{n-1}_1|}{(2\delta)^{(n-1)/2}} (1+o(1)) \qquad\text{ as }\delta\to 0. \end{align} $$
Proof Choosing coordinates so that
![]() $x=0$
and
$x=0$
and
![]() $\nu = - e_n$
, we find that locally near
$\nu = - e_n$
, we find that locally near
![]() $0$
,
$0$
,
![]() $\Omega $
has the form
$\Omega $
has the form
![]() $\{ x = (x', x_n)\in \mathbb {R}^{n-1}\times \mathbb {R}: x_n> h(x')\}$
for h such that
$\{ x = (x', x_n)\in \mathbb {R}^{n-1}\times \mathbb {R}: x_n> h(x')\}$
for h such that
![]() $h(x') = \frac 12 x'\cdot Q x'(1+o(1))$
as
$h(x') = \frac 12 x'\cdot Q x'(1+o(1))$
as
![]() $x'\to 0$
, with
$x'\to 0$
, with
![]() $\det Q = \kappa $
. From there, the definitions imply that
$\det Q = \kappa $
. From there, the definitions imply that
The expansion of h for small
![]() $x'$
implies that for any
$x'$
implies that for any
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $\delta _0>0$
such that if
$\delta _0>0$
such that if
![]() $0<\delta <\delta _0$
, then
$0<\delta <\delta _0$
, then
 $$ \begin{align*} \{x'\in \mathbb{R}^{n-1} : x'\cdot Q x' < 2\delta(1-\varepsilon) \} &\subset \{ x'\in \mathbb{R}^{n-1} : h(x') < \delta \} \\ &\subset \{x'\in \mathbb{R}^{n-1} : x'\cdot Q x' < 2\delta(1+\varepsilon) \}. \end{align*} $$
$$ \begin{align*} \{x'\in \mathbb{R}^{n-1} : x'\cdot Q x' < 2\delta(1-\varepsilon) \} &\subset \{ x'\in \mathbb{R}^{n-1} : h(x') < \delta \} \\ &\subset \{x'\in \mathbb{R}^{n-1} : x'\cdot Q x' < 2\delta(1+\varepsilon) \}. \end{align*} $$
Since the ellipse
![]() $\{ x' : x'\cdot Q x' < r^2\}$
has volume
$\{ x' : x'\cdot Q x' < r^2\}$
has volume
![]() $r^{n-1}|B^{n-1}_1|/\sqrt {\det Q}$
, we deduce (3.7) from the standard fact that
$r^{n-1}|B^{n-1}_1|/\sqrt {\det Q}$
, we deduce (3.7) from the standard fact that
![]() $|E| \, |E^\circ | = |B^{n-1}_1|^2$
for any ellipse E in
$|E| \, |E^\circ | = |B^{n-1}_1|^2$
for any ellipse E in
![]() $\mathbb {R}^{n-1}$
, a consequence of affine invariance.
$\mathbb {R}^{n-1}$
, a consequence of affine invariance.
4 Proof of Theorem 1.1
The proof of Theorem 1.1 is distributed among Propositions 4.1, 4.2, and 4.3. Before starting their proofs, we give a preliminary lemma.
Lemma 4.1 Let
![]() $E\subset \mathbb {R}^n$
denote the ellipsoid
$E\subset \mathbb {R}^n$
denote the ellipsoid
 $$\begin{align*}E := \{ x\in \mathbb{R}^n : \frac {x_1^2}{\ell_1^2} +\cdots + \frac {x_n^2}{\ell_n^2} \le 1 \}, \end{align*}$$
$$\begin{align*}E := \{ x\in \mathbb{R}^n : \frac {x_1^2}{\ell_1^2} +\cdots + \frac {x_n^2}{\ell_n^2} \le 1 \}, \end{align*}$$
let
![]() $a := (0,\ldots , 0, -\alpha )$
for some
$a := (0,\ldots , 0, -\alpha )$
for some
![]() $\alpha \in [0,\ell _n)$
, and let
$\alpha \in [0,\ell _n)$
, and let
![]() $p = (0,\ldots ,0, -\ell _n)\in \partial E$
. If
$p = (0,\ldots ,0, -\ell _n)\in \partial E$
. If
![]() $\alpha $
is close enough to
$\alpha $
is close enough to
![]() $\ell _n$
, then
$\ell _n$
, then
 $$\begin{align*}f_E(a) = \frac{ \sqrt{\kappa(p)} |B^n_1|}{ [d_{E}(a) (2 - \ell_n^{-1} d_{ E}(a))]^{(n+1)/2} }. \end{align*}$$
$$\begin{align*}f_E(a) = \frac{ \sqrt{\kappa(p)} |B^n_1|}{ [d_{E}(a) (2 - \ell_n^{-1} d_{ E}(a))]^{(n+1)/2} }. \end{align*}$$
Proof We recall that if
![]() $S\subset \mathbb {R}^n$
is a convex set, the support function
$S\subset \mathbb {R}^n$
is a convex set, the support function
![]() $\sigma _S$
is defined by
$\sigma _S$
is defined by
It is rather clear from the definitions that
Step 1. Let B denote the unit ball
![]() $B^n_1$
. Then using the properties of the support function noted above,
$B^n_1$
. Then using the properties of the support function noted above,
For a as above, by writing
![]() $y = (y', y_n)\in \mathbb {R}^{n-1}\times \mathbb {R}$
, by squaring both sides, completing a square, and rearranging, we find that
$y = (y', y_n)\in \mathbb {R}^{n-1}\times \mathbb {R}$
, by squaring both sides, completing a square, and rearranging, we find that
The inequality on the right defines an ellipsoid whose volume is easily found, yielding
Since
![]() $d_{\partial B}(a) = 1-\alpha $
, we can rewrite this as
$d_{\partial B}(a) = 1-\alpha $
, we can rewrite this as
 $$\begin{align*}f_B(a) = \frac{|B^n_1|}{ [d_{ B}(a)(2 - d_{ B}(a)]^{\frac{n+1}2}}. \end{align*}$$
$$\begin{align*}f_B(a) = \frac{|B^n_1|}{ [d_{ B}(a)(2 - d_{ B}(a)]^{\frac{n+1}2}}. \end{align*}$$
Step 2. Now let E denote a general ellipsoid as in the statement of the theorem. Noting that
we find from Lemma 2.4 that
Also, since
![]() $M^{-1}a = (0,\ldots , 0, -\alpha /\ell _n)$
, we see that
$M^{-1}a = (0,\ldots , 0, -\alpha /\ell _n)$
, we see that
![]() $d_B(M^{-1}a) = 1-\frac \alpha {\ell _n} = \frac {\ell _n-\alpha }{\ell _n}$
. Substituting into the above formula, we obtain
$d_B(M^{-1}a) = 1-\frac \alpha {\ell _n} = \frac {\ell _n-\alpha }{\ell _n}$
. Substituting into the above formula, we obtain
 $$\begin{align*}f_E(a) = \frac {\ell_n^{\frac{n-1}2}}{\ell_1\cdots\ell_{n-1}} \frac{|B^n_1|}{ [ ( \ell_n-\alpha) (2 - \frac{\ell_n-\alpha}{\ell_n})]^{\frac{n+1}2}}. \end{align*}$$
$$\begin{align*}f_E(a) = \frac {\ell_n^{\frac{n-1}2}}{\ell_1\cdots\ell_{n-1}} \frac{|B^n_1|}{ [ ( \ell_n-\alpha) (2 - \frac{\ell_n-\alpha}{\ell_n})]^{\frac{n+1}2}}. \end{align*}$$
It is clear that if
![]() $\alpha $
is close enough to
$\alpha $
is close enough to
![]() $\ell _n$
, then
$\ell _n$
, then
![]() $\ell _n-\alpha = d_{ E}(a)$
. So to complete the proof, we must show that
$\ell _n-\alpha = d_{ E}(a)$
. So to complete the proof, we must show that
![]() $\kappa (p) = \ell _n^{n-1}/(\ell _1^2\cdots \ell _{n-1}^2)$
. This is an easy computation. Near p, we write
$\kappa (p) = \ell _n^{n-1}/(\ell _1^2\cdots \ell _{n-1}^2)$
. This is an easy computation. Near p, we write
![]() $\partial E$
as the graph
$\partial E$
as the graph
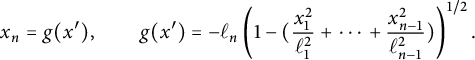 $$\begin{align*}x_n = g(x'), \qquad g(x') = -\ell_n\left(1 - ( \frac {x_1^2}{\ell_1^2} +\cdots + \frac {x_{n-1}^2}{\ell_{n-1}^2})\right)^{1/2}. \end{align*}$$
$$\begin{align*}x_n = g(x'), \qquad g(x') = -\ell_n\left(1 - ( \frac {x_1^2}{\ell_1^2} +\cdots + \frac {x_{n-1}^2}{\ell_{n-1}^2})\right)^{1/2}. \end{align*}$$
We compute that
![]() $Dg(0)=0$
and
$Dg(0)=0$
and
![]() $D^2 g(0) = \ell _n \text {diag}(\ell _1^{-2}, \ldots , \ell _{n-1}^{-2})$
, and it follows that
$D^2 g(0) = \ell _n \text {diag}(\ell _1^{-2}, \ldots , \ell _{n-1}^{-2})$
, and it follows that
![]() $\kappa (p) = \det D^2 g(0) = \ell _n^{n-1}/(\ell _1^{2} \cdots \ell _{n-1}^{2})$
, as claimed.
$\kappa (p) = \det D^2 g(0) = \ell _n^{n-1}/(\ell _1^{2} \cdots \ell _{n-1}^{2})$
, as claimed.
Proposition 4.1 Let
![]() $\Omega \subset \mathbb {R}^n$
be a bounded, convex open subset of
$\Omega \subset \mathbb {R}^n$
be a bounded, convex open subset of
![]() $\mathbb {R}^n$
for
$\mathbb {R}^n$
for
![]() $n\ge 2$
, and assume that (1.6) holds. Then
$n\ge 2$
, and assume that (1.6) holds. Then
 $$ \begin{align} \liminf_{\delta\to 0} \frac{\omega_\Omega(\delta)}{\delta^{\frac {n+1}{2n}}} \ge \left(\frac{2^{(n+1)/2}}{|B^n_1| \sqrt{\kappa_0}} \right)^{1/n}. \end{align} $$
$$ \begin{align} \liminf_{\delta\to 0} \frac{\omega_\Omega(\delta)}{\delta^{\frac {n+1}{2n}}} \ge \left(\frac{2^{(n+1)/2}}{|B^n_1| \sqrt{\kappa_0}} \right)^{1/n}. \end{align} $$
Proof Given
![]() $\varepsilon>0$
, choose a point
$\varepsilon>0$
, choose a point
![]() $p_\varepsilon \in \partial \Omega $
at which
$p_\varepsilon \in \partial \Omega $
at which
![]() $\partial \Omega $
is twice differentiable and
$\partial \Omega $
is twice differentiable and
![]() $\kappa (p_\varepsilon ) < (1+\varepsilon )\kappa _0$
. We may assume after a translation and a rotation that
$\kappa (p_\varepsilon ) < (1+\varepsilon )\kappa _0$
. We may assume after a translation and a rotation that
![]() $p_\varepsilon =0$
and that there exists
$p_\varepsilon =0$
and that there exists
![]() $r>0$
such that in a neighborhood of
$r>0$
such that in a neighborhood of
![]() $p_\varepsilon $
,
$p_\varepsilon $
,
for a convex g such that
 $$ \begin{align} g(x') = \frac 12 \sum_{j=1}^{n-1}\lambda_j x_j^2 + o(|x'|^2) \quad\text{ as } |x'|\to 0, \end{align} $$
$$ \begin{align} g(x') = \frac 12 \sum_{j=1}^{n-1}\lambda_j x_j^2 + o(|x'|^2) \quad\text{ as } |x'|\to 0, \end{align} $$
with
 $$\begin{align*}\prod_{j=1}^{n-1} \lambda_j = \kappa(p_\varepsilon) = \kappa(0), \qquad \lambda_j>0\text{ for all }j. \end{align*}$$
$$\begin{align*}\prod_{j=1}^{n-1} \lambda_j = \kappa(p_\varepsilon) = \kappa(0), \qquad \lambda_j>0\text{ for all }j. \end{align*}$$
Now let
![]() $E_\varepsilon $
be the ellipse
$E_\varepsilon $
be the ellipse
 $$\begin{align*}E_\varepsilon = \{ x\in \mathbb{R}^n : \frac {x_1^2}{\ell_1^2} + \cdots+ \frac {x_{n-1}^2}{\ell_{n-1}^2} + \frac{(x_n - \ell_n)^2}{\ell_n^2} < 1\} \end{align*}$$
$$\begin{align*}E_\varepsilon = \{ x\in \mathbb{R}^n : \frac {x_1^2}{\ell_1^2} + \cdots+ \frac {x_{n-1}^2}{\ell_{n-1}^2} + \frac{(x_n - \ell_n)^2}{\ell_n^2} < 1\} \end{align*}$$
for
 $$\begin{align*}\ell_n = \eta\text{ to be chosen}, \quad \ell_j = \left( \frac{\ell_n}{\lambda_j(1+\varepsilon)}\right)^{1/2}. \end{align*}$$
$$\begin{align*}\ell_n = \eta\text{ to be chosen}, \quad \ell_j = \left( \frac{\ell_n}{\lambda_j(1+\varepsilon)}\right)^{1/2}. \end{align*}$$
We claim that
In view of (4.2), it suffices to show that if
![]() $\eta $
is small enough and
$\eta $
is small enough and
![]() $x = (x',x_n)\in E_\varepsilon $
, then
$x = (x',x_n)\in E_\varepsilon $
, then
![]() $x\in B_r$
and
$x\in B_r$
and
![]() $x_n> g(x')$
.
$x_n> g(x')$
.
It is clear that there exists
![]() $\eta _0>0$
such that
$\eta _0>0$
such that
![]() $E_\varepsilon \subset B^n_r$
whenever
$E_\varepsilon \subset B^n_r$
whenever
![]() $0<\eta <\eta _0$
.
$0<\eta <\eta _0$
.
Second, we use the concavity of the square root to see that
 $$ \begin{align*} x\in E_\varepsilon &\quad\Longrightarrow \quad \frac{(\ell_n-x_n)^2}{\ell_n^2}\le 1 - \sum_{j=1}^{n-1} \frac {x_j^2}{\ell_j^2} \\ &\quad\Longrightarrow \quad \frac{(\ell_n-x_n)}{\ell_n}\le \left(1 - \sum_{j=1}^{n-1} \frac {x_j^2}{\ell_j^2} \right)^{1/2} \le 1 - \frac 12\sum_{j=1}^{n-1} \frac {x_j^2}{\ell_j^2} \\ &\quad\Longrightarrow \quad x_n \ge \frac 12 \sum_{j=1}^{n-1} \frac{\ell_n}{\ell_j^2} x_j^2 = \frac {(1+\varepsilon)}2 \sum_{j=1}^{n-1}\lambda_j x_j^2. \end{align*} $$
$$ \begin{align*} x\in E_\varepsilon &\quad\Longrightarrow \quad \frac{(\ell_n-x_n)^2}{\ell_n^2}\le 1 - \sum_{j=1}^{n-1} \frac {x_j^2}{\ell_j^2} \\ &\quad\Longrightarrow \quad \frac{(\ell_n-x_n)}{\ell_n}\le \left(1 - \sum_{j=1}^{n-1} \frac {x_j^2}{\ell_j^2} \right)^{1/2} \le 1 - \frac 12\sum_{j=1}^{n-1} \frac {x_j^2}{\ell_j^2} \\ &\quad\Longrightarrow \quad x_n \ge \frac 12 \sum_{j=1}^{n-1} \frac{\ell_n}{\ell_j^2} x_j^2 = \frac {(1+\varepsilon)}2 \sum_{j=1}^{n-1}\lambda_j x_j^2. \end{align*} $$
Note also that the definitions imply that
![]() $|x'| < C \sqrt \eta $
for
$|x'| < C \sqrt \eta $
for
![]() $(x',x_n)\in E_\varepsilon $
, so the above inequality and (4.3) imply that there exists
$(x',x_n)\in E_\varepsilon $
, so the above inequality and (4.3) imply that there exists
![]() $\eta _1\in (0,\eta _0)$
such that if
$\eta _1\in (0,\eta _0)$
such that if
![]() $0<\eta <\eta _1$
, then
$0<\eta <\eta _1$
, then
![]() $x_n> g(x')$
, completing the proof of (4.4).
$x_n> g(x')$
, completing the proof of (4.4).
We henceforth fix
![]() $\eta <\eta _1$
. Let
$\eta <\eta _1$
. Let
![]() $a_\delta = (0,\ldots , 0,\delta )$
for
$a_\delta = (0,\ldots , 0,\delta )$
for
![]() $\delta < \ell _n$
, and note that
$\delta < \ell _n$
, and note that
![]() $a_\delta \in E_\varepsilon $
when
$a_\delta \in E_\varepsilon $
when
![]() $\delta <2\ell _n$
. Note also that
$\delta <2\ell _n$
. Note also that
![]() $d_{\Omega }(a_\delta ) = d_{ E_\varepsilon }(a_\delta )= \delta $
for all sufficiently small
$d_{\Omega }(a_\delta ) = d_{ E_\varepsilon }(a_\delta )= \delta $
for all sufficiently small
![]() $\delta>0$
.
$\delta>0$
.
It follows from Lemma 2.2 that
![]() $f_\Omega (a_\delta )\le f_{E_\varepsilon }(a_\delta ) (a)$
, so we use (an easy modification of) Lemma 4.1 to conclude
$f_\Omega (a_\delta )\le f_{E_\varepsilon }(a_\delta ) (a)$
, so we use (an easy modification of) Lemma 4.1 to conclude
 $$\begin{align*}\lim_{\delta\searrow 0} \delta^{\frac{n+1}2}f_\Omega(a_\delta) \le \lim_{\delta\searrow 0} \delta^{\frac{n+1}2}f_{E_\varepsilon}(a_\delta) = \lim_{\delta\searrow 0} \frac {\sqrt{\kappa_{E_\varepsilon}(0)}|B^n_1|}{(2- \frac \delta {\ell_n})^{(n+1)/2}} = \frac {\sqrt{\kappa_{E_\varepsilon}(0)}|B^n_1|}{2^{(n+1)/2}}, \end{align*}$$
$$\begin{align*}\lim_{\delta\searrow 0} \delta^{\frac{n+1}2}f_\Omega(a_\delta) \le \lim_{\delta\searrow 0} \delta^{\frac{n+1}2}f_{E_\varepsilon}(a_\delta) = \lim_{\delta\searrow 0} \frac {\sqrt{\kappa_{E_\varepsilon}(0)}|B^n_1|}{(2- \frac \delta {\ell_n})^{(n+1)/2}} = \frac {\sqrt{\kappa_{E_\varepsilon}(0)}|B^n_1|}{2^{(n+1)/2}}, \end{align*}$$
where
![]() $\kappa _{E_\varepsilon }(0)$
denotes the curvature of
$\kappa _{E_\varepsilon }(0)$
denotes the curvature of
![]() $\partial E_\varepsilon $
at
$\partial E_\varepsilon $
at
![]() $0$
, which is
$0$
, which is
Applying Proposition 2.1, we find that
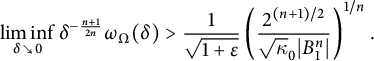 $$\begin{align*}\liminf_{\delta\searrow 0} \delta^{-\frac{n+1}{2n}} \omega_\Omega(\delta)> \frac 1{\sqrt{1+\varepsilon}} \left( \frac{2^{(n+1)/2}}{ {\sqrt \kappa_0}|B^n_1|} \right)^{1/n}. \end{align*}$$
$$\begin{align*}\liminf_{\delta\searrow 0} \delta^{-\frac{n+1}{2n}} \omega_\Omega(\delta)> \frac 1{\sqrt{1+\varepsilon}} \left( \frac{2^{(n+1)/2}}{ {\sqrt \kappa_0}|B^n_1|} \right)^{1/n}. \end{align*}$$
Since
![]() $\varepsilon>0$
was arbitrary, conclusion (4.1) follows.
$\varepsilon>0$
was arbitrary, conclusion (4.1) follows.
Proposition 4.2 Let
![]() $\Omega $
be a bounded, open, convex subset of
$\Omega $
be a bounded, open, convex subset of
![]() $\mathbb {R}^2$
satisfying (1.6). Then
$\mathbb {R}^2$
satisfying (1.6). Then
 $$\begin{align*}\sup_{\delta>0} \frac{\omega_\Omega(\delta)}{\delta^{ 3/4} }= \left( \frac {2^{3/2}}{\sqrt{\kappa_0} \pi} \right)^{1/2}. \end{align*}$$
$$\begin{align*}\sup_{\delta>0} \frac{\omega_\Omega(\delta)}{\delta^{ 3/4} }= \left( \frac {2^{3/2}}{\sqrt{\kappa_0} \pi} \right)^{1/2}. \end{align*}$$
Proof We will show that for any
![]() $a\in \Omega $
,
$a\in \Omega $
,
 $$ \begin{align} f_\Omega(a) \ge \frac 1{d_{\Omega}(a)^{ \frac 32} } \frac{ \sqrt{\kappa_0} \pi}{2^{3/2} }. \end{align} $$
$$ \begin{align} f_\Omega(a) \ge \frac 1{d_{\Omega}(a)^{ \frac 32} } \frac{ \sqrt{\kappa_0} \pi}{2^{3/2} }. \end{align} $$
In view of Proposition 2.1, this implies that
 $$\begin{align*}\sup_{\delta>0} \frac{\omega_\Omega(\delta)}{\delta^{ \frac 34 } } \le \left( \frac {2^{3/2}} {\sqrt{\kappa_0} \pi}\right)^{1/2}. \end{align*}$$
$$\begin{align*}\sup_{\delta>0} \frac{\omega_\Omega(\delta)}{\delta^{ \frac 34 } } \le \left( \frac {2^{3/2}} {\sqrt{\kappa_0} \pi}\right)^{1/2}. \end{align*}$$
This will complete the proof of the Proposition, as the opposite inequality follows from Proposition 4.1.
To prove (4.5), fix any
![]() $a\in \Omega $
, and let
$a\in \Omega $
, and let
![]() $b\in \partial \Omega $
be a point such that
$b\in \partial \Omega $
be a point such that
![]() $d_{\Omega }(a) = |a-b| =: \delta $
, not necessarily small. After a rotation and a translation, we may assume that
$d_{\Omega }(a) = |a-b| =: \delta $
, not necessarily small. After a rotation and a translation, we may assume that
![]() $b = (0,0)$
and
$b = (0,0)$
and
![]() $a = (0,\delta )$
. Clearly,
$a = (0,\delta )$
. Clearly,
![]() $B_\delta (a)\subset \Omega $
, and
$B_\delta (a)\subset \Omega $
, and
![]() $0\in \partial B_\delta (a)\cap \partial \Omega $
. From these facts and the convexity of
$0\in \partial B_\delta (a)\cap \partial \Omega $
. From these facts and the convexity of
![]() $\Omega $
, one easily sees that
$\Omega $
, one easily sees that
![]() $\Omega \subset \{ (x_1,x_2) : x_2>0\}$
and
$\Omega \subset \{ (x_1,x_2) : x_2>0\}$
and
Let
![]() $I = \{ x_1 : (x_1,x_2)\in \Omega \text { for some }x_2\}$
be the projection of
$I = \{ x_1 : (x_1,x_2)\in \Omega \text { for some }x_2\}$
be the projection of
![]() $\Omega $
onto the
$\Omega $
onto the
![]() $x_1$
-axis. Then writing the lower part of
$x_1$
-axis. Then writing the lower part of
![]() $\partial \Omega $
as the graph of a function
$\partial \Omega $
as the graph of a function
![]() $g:I\to \mathbb {R}$
, we have
$g:I\to \mathbb {R}$
, we have
Note that g is differentiable at
![]() $x_1=0$
, with
$x_1=0$
, with
![]() $g'(0)=0$
.
$g'(0)=0$
.
We now claim that
We will prove this for
![]() $x_1>0$
; the argument for
$x_1>0$
; the argument for
![]() $x_1<0$
is basically identical. Let us write
$x_1<0$
is basically identical. Let us write
![]() $S := \{ x_1\in I : g\text { is twice differentiable at }x_1\}$
. To prove (4.6), we recall assumption (1.6), which implies that
$S := \{ x_1\in I : g\text { is twice differentiable at }x_1\}$
. To prove (4.6), we recall assumption (1.6), which implies that
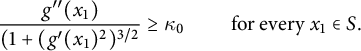 $$\begin{align*}\frac{g"(x_1)}{(1+(g'(x_1)^2)^{3/2}} \ge \kappa_0\qquad\text{ for every }x_1\in S. \end{align*}$$
$$\begin{align*}\frac{g"(x_1)}{(1+(g'(x_1)^2)^{3/2}} \ge \kappa_0\qquad\text{ for every }x_1\in S. \end{align*}$$
This clearly implies that
![]() $g"(x_1)\ge \kappa _0$
in S. Since g is convex,
$g"(x_1)\ge \kappa _0$
in S. Since g is convex,
![]() $g'$
is increasing function, so for positive
$g'$
is increasing function, so for positive
![]() $x_1\in I$
, elementary real analysis yields
$x_1\in I$
, elementary real analysis yields
Since
![]() $g'$
is locally Lipschitz, we obtain (4.6) by integrating again.
$g'$
is locally Lipschitz, we obtain (4.6) by integrating again.
In view of (4.6) and Lemma 2.2, in order to prove (4.5), it suffices to show that
 $$ \begin{align} f_D(a) = \frac {\sqrt{\kappa_0}\pi}{(2\delta)^{3/2}}. \end{align} $$
$$ \begin{align} f_D(a) = \frac {\sqrt{\kappa_0}\pi}{(2\delta)^{3/2}}. \end{align} $$
This is a straightforward computation. First, let
 $$\begin{align*}M := \left(\begin{array}{cc} \sqrt{\frac {\kappa_0}{2\delta} }&0\\ 0&\frac 1 \delta\end{array}\right). \end{align*}$$
$$\begin{align*}M := \left(\begin{array}{cc} \sqrt{\frac {\kappa_0}{2\delta} }&0\\ 0&\frac 1 \delta\end{array}\right). \end{align*}$$
Then
![]() $\widetilde D := MD = \{ (x_1, x_2) : x_2> x_1^2 \}$
and
$\widetilde D := MD = \{ (x_1, x_2) : x_2> x_1^2 \}$
and
![]() $Ma = (0,1) = e_2$
. By Lemma 2.4,
$Ma = (0,1) = e_2$
. By Lemma 2.4,
and
Given
![]() $y\in \mathbb {R}^2$
, we compute
$y\in \mathbb {R}^2$
, we compute
![]() $\sigma _{\widetilde D - e_2}(y)$
by attempting to find x that maximizes
$\sigma _{\widetilde D - e_2}(y)$
by attempting to find x that maximizes
![]() $x\mapsto y\cdot (x-e_2)$
subject to the constraint that
$x\mapsto y\cdot (x-e_2)$
subject to the constraint that
![]() $x\in \widetilde D$
. It is clear that a maximum can only occur for
$x\in \widetilde D$
. It is clear that a maximum can only occur for
![]() $x\in \partial \widetilde D$
, so one can use Lagrange multipliers to find that
$x\in \partial \widetilde D$
, so one can use Lagrange multipliers to find that
 $$\begin{align*}\sigma_{\widetilde D - e_2}(y_1,y_2) = \begin{cases} +\infty&\text{ if }y_2\ge 0\\ -\frac {y_1^2}{4y_2} - y_2 &\text{ if }y_2<0. \end{cases} \end{align*}$$
$$\begin{align*}\sigma_{\widetilde D - e_2}(y_1,y_2) = \begin{cases} +\infty&\text{ if }y_2\ge 0\\ -\frac {y_1^2}{4y_2} - y_2 &\text{ if }y_2<0. \end{cases} \end{align*}$$
It easily follows that
 $$\begin{align*}(\widetilde D-e_2)^\circ = \left\{ (y_1, y_2) : y_1^2 + 4\left(y_2-\frac 12\right)^2 \le 1\right\}, \qquad\text{ and hence, }\quad f_{\widetilde D}(e_2) = \frac \pi 2, \end{align*}$$
$$\begin{align*}(\widetilde D-e_2)^\circ = \left\{ (y_1, y_2) : y_1^2 + 4\left(y_2-\frac 12\right)^2 \le 1\right\}, \qquad\text{ and hence, }\quad f_{\widetilde D}(e_2) = \frac \pi 2, \end{align*}$$
concluding the proof of (4.7).
The remaining assertion of Theorem 1.1 is contained in the following proposition. The idea of the proof is to approximate
![]() $\partial \Omega $
from the outside, locally, by a quadratic. We need to be able to do this in a uniform way and. having done so, to extract information about
$\partial \Omega $
from the outside, locally, by a quadratic. We need to be able to do this in a uniform way and. having done so, to extract information about
![]() $\partial u_a(\Omega )$
from its quadratic approximation when this approximation is only local.
$\partial u_a(\Omega )$
from its quadratic approximation when this approximation is only local.
Proposition 4.3 If
![]() $n\ge 3$
and
$n\ge 3$
and
![]() $\partial \Omega $
is
$\partial \Omega $
is
![]() $C^2$
, then
$C^2$
, then
 $$ \begin{align} \lim_{\delta \searrow 0} \frac{\omega_\Omega(\delta)}{\delta^{(n+1)/2n} } = \left(\frac{2^{(n+1)/2}}{|B^n_1| \sqrt{\kappa_0}} \right)^{1/n}. \end{align} $$
$$ \begin{align} \lim_{\delta \searrow 0} \frac{\omega_\Omega(\delta)}{\delta^{(n+1)/2n} } = \left(\frac{2^{(n+1)/2}}{|B^n_1| \sqrt{\kappa_0}} \right)^{1/n}. \end{align} $$
Proof In view of Proposition 4.1 and Proposition 2.1, we only need to prove that
 $$ \begin{align} \liminf_{\delta\searrow 0} \inf_{d_{\Omega}(a)=\delta} \delta^{(n+1)/2} f_\Omega(a) \ge \frac{|B^n_1| \sqrt{\kappa_0}} {2^{(n+1)/2}}. \end{align} $$
$$ \begin{align} \liminf_{\delta\searrow 0} \inf_{d_{\Omega}(a)=\delta} \delta^{(n+1)/2} f_\Omega(a) \ge \frac{|B^n_1| \sqrt{\kappa_0}} {2^{(n+1)/2}}. \end{align} $$
Step 1. We first claim that for any
![]() $\varepsilon _1>0$
, there exists
$\varepsilon _1>0$
, there exists
![]() $r_0>0$
such that for any
$r_0>0$
such that for any
![]() $b \in \partial \Omega $
, there exists a rigid motion S (that is, the composition of a rotation and a translation) and a convex
$b \in \partial \Omega $
, there exists a rigid motion S (that is, the composition of a rotation and a translation) and a convex
![]() $C^2$
function
$C^2$
function
![]() $g:B^{n-1}_{r_0}\to [0,\infty )$
such that
$g:B^{n-1}_{r_0}\to [0,\infty )$
such that
and
![]() $g(0)=0$
, with
$g(0)=0$
, with
where
![]() $\| \cdot \|$
denotes the operator norm. Informally, this states that
$\| \cdot \|$
denotes the operator norm. Informally, this states that
![]() $\partial \Omega $
is uniformly
$\partial \Omega $
is uniformly
![]() $C^2$
. Since
$C^2$
. Since
![]() $\partial \Omega $
is
$\partial \Omega $
is
![]() $C^2$
and compact, on some level this is clear, but we provide some details nonetheless. Our proof of (4.10) will also show that there exist positive
$C^2$
and compact, on some level this is clear, but we provide some details nonetheless. Our proof of (4.10) will also show that there exist positive
![]() $\Lambda _{min}\le \Lambda _{max}$
, independent of
$\Lambda _{min}\le \Lambda _{max}$
, independent of
![]() $b\in \partial \Omega $
, such that
$b\in \partial \Omega $
, such that
First, the compactness of
![]() $\partial \Omega $
implies that there exists
$\partial \Omega $
implies that there exists
![]() $R>0$
,
$R>0$
,
![]() $J\ge 2$
and
$J\ge 2$
and
-
• maps
 $S_j: \mathbb {R}^n\to \mathbb {R}^n$
for
$S_j: \mathbb {R}^n\to \mathbb {R}^n$
for
 $j=1,\ldots , J$
, each one a rigid motion (the composition of a translation and a rotation),
$j=1,\ldots , J$
, each one a rigid motion (the composition of a translation and a rotation), -
•
 $C^2$
functions
$C^2$
functions
 $h_j:B_{4R}^{n-1}\to [0,\infty )$
for
$h_j:B_{4R}^{n-1}\to [0,\infty )$
for
 $j=1,\ldots , J$
,
$j=1,\ldots , J$
,
such that
![]() $|\nabla h_j| \le \frac 14$
in
$|\nabla h_j| \le \frac 14$
in
![]() $B_{4R}^{n-1}$
and
$B_{4R}^{n-1}$
and
For every j, clearly,
![]() $h_j, D h_j$
, and
$h_j, D h_j$
, and
![]() $D^2 h_j$
are uniformly continuous on
$D^2 h_j$
are uniformly continuous on
![]() $B_{3R}^{n-1}$
, and there are only finitely many of these functions, so there exists a common
$B_{3R}^{n-1}$
, and there are only finitely many of these functions, so there exists a common
![]() $C^2$
modulus of continuity for
$C^2$
modulus of continuity for
![]() $\{ h_j\}_{j=1}^J$
on
$\{ h_j\}_{j=1}^J$
on
![]() $B_{3R}^{n-1}$
, by which we mean a continuous, increasing function
$B_{3R}^{n-1}$
, by which we mean a continuous, increasing function
![]() $\mu :[0,\infty )\to [0,\infty )$
such that
$\mu :[0,\infty )\to [0,\infty )$
such that
![]() $\mu (0)=0$
and
$\mu (0)=0$
and
for all x and y in
![]() $B_{3R}^{n-1}$
and
$B_{3R}^{n-1}$
and
![]() $j=1,\ldots , J$
.
$j=1,\ldots , J$
.
Now consider any
![]() $b\in \partial \Omega $
. Fix some
$b\in \partial \Omega $
. Fix some
![]() $\bar x'\in B^{n-1}_R(0)$
and
$\bar x'\in B^{n-1}_R(0)$
and
![]() $j\in \{1,\ldots , J\}$
such that
$j\in \{1,\ldots , J\}$
such that
![]() $b = S_j(\bar x', h_j(\bar x'))$
. By a further translation, we may send
$b = S_j(\bar x', h_j(\bar x'))$
. By a further translation, we may send
![]() $(\bar x', h_j(\bar x'))$
to the origin in
$(\bar x', h_j(\bar x'))$
to the origin in
![]() $\mathbb {R}^n$
. Then by a rotation in
$\mathbb {R}^n$
. Then by a rotation in
![]() $\mathbb {R}^n$
, we can arrange that part of the (translated and rotated) graph of
$\mathbb {R}^n$
, we can arrange that part of the (translated and rotated) graph of
![]() $h_j$
over
$h_j$
over
![]() $B_{2R}(\bar x')$
can be written as the graph over some ball
$B_{2R}(\bar x')$
can be written as the graph over some ball
![]() $B_{r}^{n-1}$
of a convex
$B_{r}^{n-1}$
of a convex
![]() $C^2$
function
$C^2$
function
![]() $g:B^{n-1}_r\to [0,\infty )$
such that
$g:B^{n-1}_r\to [0,\infty )$
such that
![]() $g(0)=0$
and
$g(0)=0$
and
![]() $\nabla g(0)=0$
. By applying Lemma 4.2 below to
$\nabla g(0)=0$
. By applying Lemma 4.2 below to
![]() $h(x') = h_j(x' - \bar x') - h_j(\bar x')$
, we find that independent of the choice of b, the domain of the resulting function g can be taken to be
$h(x') = h_j(x' - \bar x') - h_j(\bar x')$
, we find that independent of the choice of b, the domain of the resulting function g can be taken to be
![]() $B^{n-1}_R$
, and g has a
$B^{n-1}_R$
, and g has a
![]() $C^2$
modulus of continuity in
$C^2$
modulus of continuity in
![]() $B_R^{n-1}$
that can be estimated solely in terms of
$B_R^{n-1}$
that can be estimated solely in terms of
![]() $\mu $
from (4.12). This proves (4.10). Similarly, (4.11) follows from (4.25) in Lemma 4.2, which we prove below, together with the fact that for every
$\mu $
from (4.12). This proves (4.10). Similarly, (4.11) follows from (4.25) in Lemma 4.2, which we prove below, together with the fact that for every
![]() $j\in \{1,\ldots ,J\}$
, the eigenvalues of
$j\in \{1,\ldots ,J\}$
, the eigenvalues of
![]() $D^2 h_j$
are bounded away from
$D^2 h_j$
are bounded away from
![]() $0$
in
$0$
in
![]() $B^{n-1}_R$
, being positive on
$B^{n-1}_R$
, being positive on
![]() $B^{n-1}_{2R}$
.
$B^{n-1}_{2R}$
.
Step 2. We now prove (4.9).
Step 2.1: Normalization and approximation by a quadratic. Because
![]() $\partial \Omega $
is
$\partial \Omega $
is
![]() $C^2$
and compact, there exists
$C^2$
and compact, there exists
![]() $\delta _0>0$
such that if
$\delta _0>0$
such that if
![]() $\delta := d_{\Omega }(a) <\delta _0$
, then there is a unique
$\delta := d_{\Omega }(a) <\delta _0$
, then there is a unique
![]() $b\in \partial \Omega $
such that
$b\in \partial \Omega $
such that
![]() $d_{\Omega }(a)=|a-b|$
. Fix some such a and b. In view of Step 1, we may assume after a rigid motion that
$d_{\Omega }(a)=|a-b|$
. Fix some such a and b. In view of Step 1, we may assume after a rigid motion that
![]() $a = \delta e_n = (0,\ldots , 0,\delta )$
and
$a = \delta e_n = (0,\ldots , 0,\delta )$
and
![]() $b=0$
, and that there is a nonnegative convex function g, vanishing at
$b=0$
, and that there is a nonnegative convex function g, vanishing at
![]() $x'=0$
, such that (4.10) holds for some
$x'=0$
, such that (4.10) holds for some
![]() $\varepsilon _1$
and
$\varepsilon _1$
and
![]() $r_0(\varepsilon _1)$
to be specified in a moment, and with
$r_0(\varepsilon _1)$
to be specified in a moment, and with
![]() $\{(x', g(x')) : |x'|<r_0\}$
contained in the (rotated and translated)
$\{(x', g(x')) : |x'|<r_0\}$
contained in the (rotated and translated)
![]() $\partial \Omega $
.
$\partial \Omega $
.
Fix
![]() $\varepsilon>0$
. Using (4.10) for a suitably small choice of
$\varepsilon>0$
. Using (4.10) for a suitably small choice of
![]() $\varepsilon _1$
and calculus, we can guarantee that
$\varepsilon _1$
and calculus, we can guarantee that
 $$ \begin{align} \left. \begin{aligned} g(x')> \frac {(1-\varepsilon)}2 x'\cdot Qx' &\\ |Dg(x') - Q x'| < \varepsilon |x'| & \end{aligned}\right\} \ \text{ in }B_{r_0}^{n-1}, \quad\text{ for }Q = D^2g(0). \end{align} $$
$$ \begin{align} \left. \begin{aligned} g(x')> \frac {(1-\varepsilon)}2 x'\cdot Qx' &\\ |Dg(x') - Q x'| < \varepsilon |x'| & \end{aligned}\right\} \ \text{ in }B_{r_0}^{n-1}, \quad\text{ for }Q = D^2g(0). \end{align} $$
Let
![]() $M:= Q^{1/2}$
, the positive definite symmetric square root of Q, and define
$M:= Q^{1/2}$
, the positive definite symmetric square root of Q, and define
 $$\begin{align*}\widetilde \Omega := \left\{ \left(\frac {M x'}{\sqrt \delta}, \frac{x_n}\delta \right) : (x', x_n)\in \Omega\right\}, \qquad \tilde g(y') := \frac 1 \delta g(\sqrt \delta M^{-1} y'). \end{align*}$$
$$\begin{align*}\widetilde \Omega := \left\{ \left(\frac {M x'}{\sqrt \delta}, \frac{x_n}\delta \right) : (x', x_n)\in \Omega\right\}, \qquad \tilde g(y') := \frac 1 \delta g(\sqrt \delta M^{-1} y'). \end{align*}$$
Due to (4.11), the eigenvalues of M are bounded between
![]() $ \Lambda _{min}^{1/2}$
and
$ \Lambda _{min}^{1/2}$
and
![]() $\Lambda _{max}^{1/2}$
. Thus,
$\Lambda _{max}^{1/2}$
. Thus,
The definition of
![]() $\widetilde g$
is chosen so that
$\widetilde g$
is chosen so that
Hypothesis (1.6) implies that
![]() $\det Q = (\text {curvature of }\partial \Omega \text { at }b=0) \ge \kappa _0$
, so we deduce from Lemma 2.4 that
$\det Q = (\text {curvature of }\partial \Omega \text { at }b=0) \ge \kappa _0$
, so we deduce from Lemma 2.4 that
In addition, using (4.14) and requiring that
![]() $\varepsilon < \frac 12 \Lambda _{min}$
, we can translate properties (4.13) into statements about
$\varepsilon < \frac 12 \Lambda _{min}$
, we can translate properties (4.13) into statements about
![]() $\tilde g$
. It follows that
$\tilde g$
. It follows that
![]() $(y',\tilde g(y'))\in \partial \widetilde \Omega $
and
$(y',\tilde g(y'))\in \partial \widetilde \Omega $
and
 $$ \begin{align} \left. \begin{aligned} \tilde g(y')> \frac {(1-\varepsilon)}2 |y'|^2 & \\ |D\tilde g(y') - y'| < \varepsilon \Lambda_{min}^{-1} |y'| <\frac 12 |y'| & \end{aligned}\right\} \text{ in }B_{r_\delta}^{n-1}. \end{align} $$
$$ \begin{align} \left. \begin{aligned} \tilde g(y')> \frac {(1-\varepsilon)}2 |y'|^2 & \\ |D\tilde g(y') - y'| < \varepsilon \Lambda_{min}^{-1} |y'| <\frac 12 |y'| & \end{aligned}\right\} \text{ in }B_{r_\delta}^{n-1}. \end{align} $$
Fix
![]() $z'$
such that
$z'$
such that
![]() $|z'|< r_\delta /2$
and let
$|z'|< r_\delta /2$
and let
![]() $\Phi (y') := z'+y' - D\tilde g(y')$
. Then the second inequality in (4.16) implies that
$\Phi (y') := z'+y' - D\tilde g(y')$
. Then the second inequality in (4.16) implies that
![]() $\Phi $
maps
$\Phi $
maps
![]() $\bar B_{r_2}^{n-1}$
to itself, for
$\bar B_{r_2}^{n-1}$
to itself, for
![]() $r_2 = 2|z'| < r_\delta $
. Thus, the Brouwer Fixed Point Theorem implies that
$r_2 = 2|z'| < r_\delta $
. Thus, the Brouwer Fixed Point Theorem implies that
![]() $\Phi $
has a fixed point
$\Phi $
has a fixed point
![]() $y'$
in
$y'$
in
![]() $B_{r_2}^{n-1}$
. But
$B_{r_2}^{n-1}$
. But
![]() $\Phi (y') =y'$
exactly when
$\Phi (y') =y'$
exactly when
![]() $D\tilde g(y') = z'$
. It follows that
$D\tilde g(y') = z'$
. It follows that
Step 2.2: finding a large subset of
![]() $\partial u_{\widetilde \Omega , a}(\tilde \Omega )$
.
$\partial u_{\widetilde \Omega , a}(\tilde \Omega )$
.
We will write
![]() $\tilde u_{\tilde a} := u_{\widetilde \Omega , \tilde a}$
. We next will show that
$\tilde u_{\tilde a} := u_{\widetilde \Omega , \tilde a}$
. We next will show that
 $$ \begin{align} E_{\varepsilon,\delta} := \left\{ s( z', -1) :|z'|< \frac {r_\delta}2, \ \ 0\le s \le \left( 1 + \frac 1{2(1-\varepsilon)} |z'|^2 \right)^{-1} \right \} \subset \partial \tilde u_{\tilde a}(\widetilde \Omega). \end{align} $$
$$ \begin{align} E_{\varepsilon,\delta} := \left\{ s( z', -1) :|z'|< \frac {r_\delta}2, \ \ 0\le s \le \left( 1 + \frac 1{2(1-\varepsilon)} |z'|^2 \right)^{-1} \right \} \subset \partial \tilde u_{\tilde a}(\widetilde \Omega). \end{align} $$
To see this, fix
![]() $z'\in B^{n-1}_{r_\delta /2}$
, and using (4.17), find
$z'\in B^{n-1}_{r_\delta /2}$
, and using (4.17), find
![]() $y'\in B^{n-1}_{r_\delta }$
such that
$y'\in B^{n-1}_{r_\delta }$
such that
![]() $\nabla \tilde g(y') = z'$
. Let
$\nabla \tilde g(y') = z'$
. Let
 $$\begin{align*}\ell_{y'}(x) := \frac{ (\nabla \tilde g(y'), -1) \cdot(x - (y', \tilde g(y')))} {1 + y'\cdot \nabla \tilde g(y')- \tilde g(y')}. \end{align*}$$
$$\begin{align*}\ell_{y'}(x) := \frac{ (\nabla \tilde g(y'), -1) \cdot(x - (y', \tilde g(y')))} {1 + y'\cdot \nabla \tilde g(y')- \tilde g(y')}. \end{align*}$$
We claim that
![]() $\ell _{y'}$
is a supporting hyperplane to the graph of
$\ell _{y'}$
is a supporting hyperplane to the graph of
![]() $\tilde u_{\tilde a}$
at
$\tilde u_{\tilde a}$
at
![]() $\tilde a =e_n$
. We must show that
$\tilde a =e_n$
. We must show that
![]() $\ell _{y'}(\tilde a) = \tilde u_{\tilde a}(\tilde a) = -1$
, which follows directly from the definition, and that
$\ell _{y'}(\tilde a) = \tilde u_{\tilde a}(\tilde a) = -1$
, which follows directly from the definition, and that
![]() $\ell _a \le \tilde u_{\tilde a}$
in
$\ell _a \le \tilde u_{\tilde a}$
in
![]() $\widetilde \Omega $
. Since both
$\widetilde \Omega $
. Since both
![]() $\ell _a$
and
$\ell _a$
and
![]() $\tilde u_{\tilde a}$
are linear on line segments connecting
$\tilde u_{\tilde a}$
are linear on line segments connecting
![]() $\partial \widetilde \Omega $
to
$\partial \widetilde \Omega $
to
![]() $\tilde a$
, it suffices to check that
$\tilde a$
, it suffices to check that
![]() $\ell _a \le \tilde u_{\tilde a} = 0$
on
$\ell _a \le \tilde u_{\tilde a} = 0$
on
![]() $\partial \widetilde \Omega $
. This follows from noting that
$\partial \widetilde \Omega $
. This follows from noting that
![]() $\ell _{y'}$
vanishes exactly on the hyperplane
$\ell _{y'}$
vanishes exactly on the hyperplane
![]() $\{ x\in \mathbb {R}^n : \nu (y) \cdot (x - y) = 0\}$
, where
$\{ x\in \mathbb {R}^n : \nu (y) \cdot (x - y) = 0\}$
, where
![]() $y = (y', \tilde g(y'))\in \partial \widetilde \Omega $
and
$y = (y', \tilde g(y'))\in \partial \widetilde \Omega $
and
![]() $\nu (y)$
is the outer unit normal to
$\nu (y)$
is the outer unit normal to
![]() $\partial \widetilde \Omega $
at y. This is a supporting hyperplane to
$\partial \widetilde \Omega $
at y. This is a supporting hyperplane to
![]() $\partial \widetilde \Omega $
, so
$\partial \widetilde \Omega $
, so
![]() $\ell _{y'}$
does not change sign in
$\ell _{y'}$
does not change sign in
![]() $\widetilde \Omega $
. Since
$\widetilde \Omega $
. Since
![]() $\ell _{y'}(\tilde a)<0$
, the claim follows.
$\ell _{y'}(\tilde a)<0$
, the claim follows.
Thus,
![]() $\nabla \ell _{y'}(\tilde a)\in \partial \tilde u_{\tilde a}(\tilde a)$
. Since it is clear that
$\nabla \ell _{y'}(\tilde a)\in \partial \tilde u_{\tilde a}(\tilde a)$
. Since it is clear that
![]() $0\in \partial \tilde u_{\tilde a}(\tilde a)$
and
$0\in \partial \tilde u_{\tilde a}(\tilde a)$
and
![]() $\partial \tilde u_{\tilde a}(\tilde a)$
is convex, it follows that the segment
$\partial \tilde u_{\tilde a}(\tilde a)$
is convex, it follows that the segment
![]() $\{ s\nabla \ell _{y'}(\tilde a) : 0\le s \le 1\} \subset \partial \tilde u_{\tilde a}(\tilde a)$
; that is,
$\{ s\nabla \ell _{y'}(\tilde a) : 0\le s \le 1\} \subset \partial \tilde u_{\tilde a}(\tilde a)$
; that is,
 $$ \begin{align} \left\{ s(\nabla\tilde g(y') , -1) \ : \ 0 \le s \le \frac 1{1+y'\cdot \nabla\tilde g(y')-\tilde g(y')} \right \} \subset \partial \tilde u_{\tilde a}(a). \end{align} $$
$$ \begin{align} \left\{ s(\nabla\tilde g(y') , -1) \ : \ 0 \le s \le \frac 1{1+y'\cdot \nabla\tilde g(y')-\tilde g(y')} \right \} \subset \partial \tilde u_{\tilde a}(a). \end{align} $$
However, recalling that
![]() $\nabla \tilde g(y') = z'$
, and using (4.16) and elementary inequalities,
$\nabla \tilde g(y') = z'$
, and using (4.16) and elementary inequalities,
 $$\begin{align*}y'\cdot \nabla \tilde g(y') - \tilde g(y') \le y'\cdot z' - \frac {(1-\varepsilon)}2|y'|^2 \le \frac 1{2(1-\varepsilon)}|z'|^2. \end{align*}$$
$$\begin{align*}y'\cdot \nabla \tilde g(y') - \tilde g(y') \le y'\cdot z' - \frac {(1-\varepsilon)}2|y'|^2 \le \frac 1{2(1-\varepsilon)}|z'|^2. \end{align*}$$
We deduce (4.18) by combining this and (4.19).
Step 2.3: conclusion of proof. Since a was an arbitrary point such that
![]() $d_{\Omega }(a)=\delta $
, it follows from (4.18) and (4.15) that for all sufficiently small
$d_{\Omega }(a)=\delta $
, it follows from (4.18) and (4.15) that for all sufficiently small
![]() $\delta $
,
$\delta $
,
We will show that
Since
![]() $\varepsilon>0$
is arbitrary, this and (4.20) imply (4.9) and thus complete the proof of the Proposition.
$\varepsilon>0$
is arbitrary, this and (4.20) imply (4.9) and thus complete the proof of the Proposition.
To establish (4.21), note first that
![]() $E_{\varepsilon ,\delta }$
forms an increasing family of sets as
$E_{\varepsilon ,\delta }$
forms an increasing family of sets as
![]() $\delta \searrow 0$
. Thus, the Monotone Convergence Theorem implies that
$\delta \searrow 0$
. Thus, the Monotone Convergence Theorem implies that
![]() $\lim _{\delta \to 0}|E_{\varepsilon ,\delta }| = |E_{\varepsilon ,0}|$
, for
$\lim _{\delta \to 0}|E_{\varepsilon ,\delta }| = |E_{\varepsilon ,0}|$
, for
 $$\begin{align*}E_{\varepsilon,0} := \cup_{\delta>0} E_{\varepsilon,\delta} = \left\{ s(p', -1) \,:\ p'\in \mathbb{R}^{n-1}, \ 0 \le s \le \left(1 + \frac 1{2(1-\varepsilon)} |p'|^2 \right)^{-1} \right\}. \end{align*}$$
$$\begin{align*}E_{\varepsilon,0} := \cup_{\delta>0} E_{\varepsilon,\delta} = \left\{ s(p', -1) \,:\ p'\in \mathbb{R}^{n-1}, \ 0 \le s \le \left(1 + \frac 1{2(1-\varepsilon)} |p'|^2 \right)^{-1} \right\}. \end{align*}$$
We claim that, in fact,
 $$ \begin{align} E_{\varepsilon,0} = \left\{ (q', q_n) \in \mathbb{R}^n : \frac 2{(1-\varepsilon)}|q'|^2 + 4(q_n +\frac 12)^2 \le 1 \right\} =: \mathcal E_{\varepsilon,0}. \end{align} $$
$$ \begin{align} E_{\varepsilon,0} = \left\{ (q', q_n) \in \mathbb{R}^n : \frac 2{(1-\varepsilon)}|q'|^2 + 4(q_n +\frac 12)^2 \le 1 \right\} =: \mathcal E_{\varepsilon,0}. \end{align} $$
Indeed, both
![]() $\mathcal E_{\varepsilon ,0}$
and
$\mathcal E_{\varepsilon ,0}$
and
![]() $E_{\varepsilon ,0}$
are contained in the set
$E_{\varepsilon ,0}$
are contained in the set
![]() $\{ 0\} \cup \{(q', q_n) : q_n < 0\}$
. It is clear that the origin belongs to both sets. Any point with
$\{ 0\} \cup \{(q', q_n) : q_n < 0\}$
. It is clear that the origin belongs to both sets. Any point with
![]() $(q', q_n)$
with
$(q', q_n)$
with
![]() $q_n<0$
can be written
$q_n<0$
can be written
 $$ \begin{align} (q', q_n) = \frac{ t(p',-1)}{1 + \frac 1{2(1-\varepsilon)} |p'|^2 } \qquad\text{ for some }p'\in \mathbb{R}^{n-1}\text{ and }t>0. \end{align} $$
$$ \begin{align} (q', q_n) = \frac{ t(p',-1)}{1 + \frac 1{2(1-\varepsilon)} |p'|^2 } \qquad\text{ for some }p'\in \mathbb{R}^{n-1}\text{ and }t>0. \end{align} $$
Then
 $$\begin{align*}|q'|^2 = t^2 \frac{|p'|^2}{(1 + \frac 1{2(1-\varepsilon)} |p'|^2)^2} \end{align*}$$
$$\begin{align*}|q'|^2 = t^2 \frac{|p'|^2}{(1 + \frac 1{2(1-\varepsilon)} |p'|^2)^2} \end{align*}$$
and
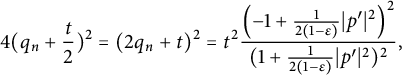 $$\begin{align*}4(q_n+\frac t2)^2 = (2q_n+t)^2 = t^2 \frac{\left( -1+ \frac 1{2(1-\varepsilon)} |p'|^2\right)^2}{(1 + \frac 1{2(1-\varepsilon)} |p'|^2)^2}, \end{align*}$$
$$\begin{align*}4(q_n+\frac t2)^2 = (2q_n+t)^2 = t^2 \frac{\left( -1+ \frac 1{2(1-\varepsilon)} |p'|^2\right)^2}{(1 + \frac 1{2(1-\varepsilon)} |p'|^2)^2}, \end{align*}$$
from which we see that
One then checks that
For
![]() $q_n<0$
, the right-hand side is larger than
$q_n<0$
, the right-hand side is larger than
![]() $1$
if and only if
$1$
if and only if
![]() $t>1$
. Thus,
$t>1$
. Thus,
Since
![]() $(q', q_n)\in E_{\varepsilon ,0}$
if and only if
$(q', q_n)\in E_{\varepsilon ,0}$
if and only if
![]() $0<t\le 1$
in (4.23), this implies (4.22).
$0<t\le 1$
in (4.23), this implies (4.22).
And it is clear that
![]() $|\mathcal E_{\varepsilon ,0}|= \frac {(1-\varepsilon )^{(n-1)/2}|B^n_1|}{2^{(n+1)/2}}$
, proving (4.21).
$|\mathcal E_{\varepsilon ,0}|= \frac {(1-\varepsilon )^{(n-1)/2}|B^n_1|}{2^{(n+1)/2}}$
, proving (4.21).
Finally, we establish the lemma used above. In the proof, we find it helpful to write points
![]() $x = (x', x_n)\in \mathbb {R}^n = \mathbb {R}^{n-1}\times \mathbb {R}$
as column vectors
$x = (x', x_n)\in \mathbb {R}^n = \mathbb {R}^{n-1}\times \mathbb {R}$
as column vectors
![]() $\binom {x'}{x_n}$
.
$\binom {x'}{x_n}$
.
Lemma 4.2 Let
![]() $h\in C^2(B^{n-1}_{2R})$
satisfy
$h\in C^2(B^{n-1}_{2R})$
satisfy
![]() $h(0)= 0$
and
$h(0)= 0$
and
![]() $\| \nabla h\|_{L^\infty } \le \frac 14$
.
$\| \nabla h\|_{L^\infty } \le \frac 14$
.
Then there exists a rotation
![]() $S\in SO(n)$
and a function
$S\in SO(n)$
and a function
![]() $g\in C^2(B^{n-1}_R)$
such that
$g\in C^2(B^{n-1}_R)$
such that
![]() $\nabla g(0)=0$
,
$\nabla g(0)=0$
,
 $$ \begin{align} \left\{ \binom{y'}{ g(y')} : |y'| < R \right\} \subset \left\{ S\binom{x'}{ h(x')} : |x'|<20R/11 \right\}, \end{align} $$
$$ \begin{align} \left\{ \binom{y'}{ g(y')} : |y'| < R \right\} \subset \left\{ S\binom{x'}{ h(x')} : |x'|<20R/11 \right\}, \end{align} $$
and such that the
![]() $C^2$
modulus of continuity of g can be estimated in terms only of the
$C^2$
modulus of continuity of g can be estimated in terms only of the
![]() $C^2$
modulus of continuity of h in
$C^2$
modulus of continuity of h in
![]() $B^{n-1}_{20R/11}$
. Moreover,
$B^{n-1}_{20R/11}$
. Moreover,
 $$ \begin{align} g_{y_i y_j}(0) = \begin{cases} (1+m^2)^{-1/2} h_{x_i x_j}(0) &\text{ if }i,j\le n-2\\ (1+m^2)^{-1}h_{x_i x_j}(0) &\text{ if }i<j=n-1\text{ or }j<i=n-1\\ (1+m^2)^{-3/2} h_{x_i x_j}(0) &\text{ if } i=j =n-1\,,\end{cases} \end{align} $$
$$ \begin{align} g_{y_i y_j}(0) = \begin{cases} (1+m^2)^{-1/2} h_{x_i x_j}(0) &\text{ if }i,j\le n-2\\ (1+m^2)^{-1}h_{x_i x_j}(0) &\text{ if }i<j=n-1\text{ or }j<i=n-1\\ (1+m^2)^{-3/2} h_{x_i x_j}(0) &\text{ if } i=j =n-1\,,\end{cases} \end{align} $$
for some
![]() $m \in [-\frac {1}{4},\frac {1}{4}]$
, and if h is convex, then g is convex.
$m \in [-\frac {1}{4},\frac {1}{4}]$
, and if h is convex, then g is convex.
The conclusion of the lemma is a little stronger than we need for the proof of Proposition 4.3.
Proof We may assume by a suitable choice of coordinates that
![]() $\nabla h (0) = m e_{n-1}$
for some
$\nabla h (0) = m e_{n-1}$
for some
![]() $m\in [-\frac 14, \frac 14]$
, where
$m\in [-\frac 14, \frac 14]$
, where
![]() $e_{n-1}$
is the standard basis vector along the
$e_{n-1}$
is the standard basis vector along the
![]() $x_{n-1}$
axis.
$x_{n-1}$
axis.
We then define (temporarily adopting column vector notation for ease of reading)
 $$\begin{align*}S\left(\begin{array}{c}x_1\\ \vdots \\ x_{n-2} \\ x_{n-1} \\ x_n\end{array}\right) = \left(\begin{array}{c}x_1\\ \vdots \\ x_{n-2} \\ \alpha x_{n-1}+\beta x_n \\ -\beta x_{n-1} + \alpha x_n\end{array}\right), \qquad \alpha = \frac 1{\sqrt {1+m^2}}, \quad \beta = \frac m{\sqrt {1+m^2}}. \end{align*}$$
$$\begin{align*}S\left(\begin{array}{c}x_1\\ \vdots \\ x_{n-2} \\ x_{n-1} \\ x_n\end{array}\right) = \left(\begin{array}{c}x_1\\ \vdots \\ x_{n-2} \\ \alpha x_{n-1}+\beta x_n \\ -\beta x_{n-1} + \alpha x_n\end{array}\right), \qquad \alpha = \frac 1{\sqrt {1+m^2}}, \quad \beta = \frac m{\sqrt {1+m^2}}. \end{align*}$$
Clearly,
![]() $S\in SO(n)$
. Note that
$S\in SO(n)$
. Note that
![]() $\alpha \ge 4/\sqrt {17}> 4/5$
and
$\alpha \ge 4/\sqrt {17}> 4/5$
and
![]() $|\beta |\le 1/\sqrt {17} < 1/4$
. We next define
$|\beta |\le 1/\sqrt {17} < 1/4$
. We next define
![]() $\Phi :B_{2R}^{n-1} \to \mathbb {R}^n$
$\Phi :B_{2R}^{n-1} \to \mathbb {R}^n$
 $$\begin{align*}S \binom{x'}{h(x')} =: \Phi(x') = \binom {\phi(x')}{\phi^n(x')}, \end{align*}$$
$$\begin{align*}S \binom{x'}{h(x')} =: \Phi(x') = \binom {\phi(x')}{\phi^n(x')}, \end{align*}$$
where we will write the components of
![]() $\phi $
as
$\phi $
as
![]() $(\phi ^1,\ldots , \phi ^{n-1})$
, for
$(\phi ^1,\ldots , \phi ^{n-1})$
, for
![]() $\phi $
and
$\phi $
and
![]() $\phi ^n$
taking values in
$\phi ^n$
taking values in
![]() $\mathbb {R}^{n-1}$
and
$\mathbb {R}^{n-1}$
and
![]() $\mathbb {R}$
, respectively. We now define
$\mathbb {R}$
, respectively. We now define
We now verify that these functions have the stated properties.
Proof that g is well-defined on
![]() $B_R^{n-1}$
: From the definitions, we see that
$B_R^{n-1}$
: From the definitions, we see that
Thus, writing
![]() $\| A\|$
to denote the operator norm of a matrix A and
$\| A\|$
to denote the operator norm of a matrix A and
![]() $I_k$
the
$I_k$
the
![]() $k\times k$
identity matrix, we check that
$k\times k$
identity matrix, we check that
Now fix any
![]() $y'\in B_R^{n-1}$
, and define
$y'\in B_R^{n-1}$
, and define
![]() $\Phi (x') = y'+x' -\phi (x')$
. Then for any
$\Phi (x') = y'+x' -\phi (x')$
. Then for any
![]() $x', z'\in B_{2R}^{n-1}$
,
$x', z'\in B_{2R}^{n-1}$
,
 $$ \begin{align} \left|\Phi(x') - \Phi(z')\right| =\left| \int_0^1 \frac d{ds}\Phi(s x'+(1-s )z')\,ds\right| &\le \sup_{B^{n-1}_{2R}} \| D\phi - I_{n-1} \| \, |x'-z'| \nonumber \\ & \le \frac 9{20}|x'-z'|. \end{align} $$
$$ \begin{align} \left|\Phi(x') - \Phi(z')\right| =\left| \int_0^1 \frac d{ds}\Phi(s x'+(1-s )z')\,ds\right| &\le \sup_{B^{n-1}_{2R}} \| D\phi - I_{n-1} \| \, |x'-z'| \nonumber \\ & \le \frac 9{20}|x'-z'|. \end{align} $$
Thus,
![]() $\Phi $
is a contraction mapping. Note also, that when
$\Phi $
is a contraction mapping. Note also, that when
![]() $y=0$
, we find from (4.28) that
$y=0$
, we find from (4.28) that
![]() $|\phi (x')-x'| \le \frac 9{20}|x'|$
. So if
$|\phi (x')-x'| \le \frac 9{20}|x'|$
. So if
![]() $|x'| \le 20R/11$
, then
$|x'| \le 20R/11$
, then
So
![]() $\Phi $
maps
$\Phi $
maps
![]() $B^{n-1}_{20R/11}$
to itself, and the Contraction Mapping Principle thus implies that there is a unique
$B^{n-1}_{20R/11}$
to itself, and the Contraction Mapping Principle thus implies that there is a unique
![]() $z'\in B^{n-1}_{20R/11}$
such that
$z'\in B^{n-1}_{20R/11}$
such that
![]() $\Phi (z') = z'$
, which says exactly that
$\Phi (z') = z'$
, which says exactly that
![]() $\phi (z') = y'$
.
$\phi (z') = y'$
.
These facts imply that
![]() $\phi ^{-1} =\psi $
is well-defined in
$\phi ^{-1} =\psi $
is well-defined in
![]() $B^{n-1}_R$
, taking values in
$B^{n-1}_R$
, taking values in
![]() $B^{n-1}_{20R/11}$
, and hence that g is well-defined in
$B^{n-1}_{20R/11}$
, and hence that g is well-defined in
![]() $B^{n-1}_R$
as well.
$B^{n-1}_R$
as well.
Proof that (4.24) holds: The definitions imply that if
![]() $y' = \phi (x')$
, then
$y' = \phi (x')$
, then
![]() $g(y') = \phi ^n(x')$
, and thus,
$g(y') = \phi ^n(x')$
, and thus,
 $$\begin{align*}\binom {y'}{g(y')} = \binom{\phi(x')}{\phi^n(x')} = \Phi(x') = S\binom {x'}{h(x')}. \end{align*}$$
$$\begin{align*}\binom {y'}{g(y')} = \binom{\phi(x')}{\phi^n(x')} = \Phi(x') = S\binom {x'}{h(x')}. \end{align*}$$
We deduce (4.24) from this and remarks above about the range of
![]() $\psi $
.
$\psi $
.
Proof that
![]() $\nabla g(0)=0$
: We compute
$\nabla g(0)=0$
: We compute
Since
![]() $\phi (0)=0$
, it is clear that
$\phi (0)=0$
, it is clear that
![]() $\psi (0)=0$
. It thus suffices to check that
$\psi (0)=0$
. It thus suffices to check that
![]() $\nabla \phi ^n (0)=0$
. This follows from the choice of
$\nabla \phi ^n (0)=0$
. This follows from the choice of
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
, which guarantees that
$\beta $
, which guarantees that
 $$\begin{align*}\phi^n_{x_k}(0) = \begin{cases} \alpha h_{x_k}(0) = 0&\text{ if }k\le n-2\\ -\beta + \alpha h_{x_{n-1}}(0) = 0&\text{ if }k=n-1. \end{cases}\end{align*}$$
$$\begin{align*}\phi^n_{x_k}(0) = \begin{cases} \alpha h_{x_k}(0) = 0&\text{ if }k\le n-2\\ -\beta + \alpha h_{x_{n-1}}(0) = 0&\text{ if }k=n-1. \end{cases}\end{align*}$$
![]() $C^2$
modulus of continuity of g: By differentiating (4.29), we obtain
$C^2$
modulus of continuity of g: By differentiating (4.29), we obtain
Moreover,
For every
![]() $x'\in B_{2R}^{n-1}$
, it follows from (4.27) that
$x'\in B_{2R}^{n-1}$
, it follows from (4.27) that
![]() $D\phi (x')$
belongs to the compact set
$D\phi (x')$
belongs to the compact set
![]() $\{ A\in M^{n-1} : \| A - I\| \le 9/20 \}$
on which the map
$\{ A\in M^{n-1} : \| A - I\| \le 9/20 \}$
on which the map
![]() $A\mapsto A^{-1}$
is smooth and hence bounded and Lipschitz. Hence,
$A\mapsto A^{-1}$
is smooth and hence bounded and Lipschitz. Hence,
![]() $D\psi $
is bounded in
$D\psi $
is bounded in
![]() $B_R^{n-1}$
, and
$B_R^{n-1}$
, and
![]() $\psi $
is Lipschitz continuous. Then elementary estimates show that first
$\psi $
is Lipschitz continuous. Then elementary estimates show that first
![]() $D\psi $
and then
$D\psi $
and then
![]() $D^2\psi $
have moduli of continuity estimated only in terms of the
$D^2\psi $
have moduli of continuity estimated only in terms of the
![]() $C^2$
modulus of continuity of
$C^2$
modulus of continuity of
![]() $\phi $
, which in turn is controlled by the
$\phi $
, which in turn is controlled by the
![]() $C^2$
modulus of continuity of h. Then similar arguments show that the
$C^2$
modulus of continuity of h. Then similar arguments show that the
![]() $C^2$
modulus of continuity of g can be estimated only in terms of that of h.
$C^2$
modulus of continuity of g can be estimated only in terms of that of h.
Formula for
![]() $D^2 g(0)$
. Computing as in our verification that
$D^2 g(0)$
. Computing as in our verification that
![]() $\nabla g(0)=\nabla \phi ^n(0)=0$
, and recalling that
$\nabla g(0)=\nabla \phi ^n(0)=0$
, and recalling that
![]() $\psi (0)=0$
, one easily checks that
$\psi (0)=0$
, one easily checks that
![]() $D^2 \phi ^n(0) = \alpha D^2 h(0)$
. Similarly, nothing from the definitions that
$D^2 \phi ^n(0) = \alpha D^2 h(0)$
. Similarly, nothing from the definitions that
![]() $\partial _{n-1}\phi ^{n-1}(0) = \alpha +\beta m = 1/\alpha $
, one checks that
$\partial _{n-1}\phi ^{n-1}(0) = \alpha +\beta m = 1/\alpha $
, one checks that
We deduce (4.25) from these facts and (4.30).
Finally, it is clear that if h is convex, then g is convex, as then the graph of g is part of the lower boundary of a convex set.
Acknowledgements
This work was partially supported by the Natural Sciences and Engineering Research Council of Canada under Operating Grant 261955. In addition, the research of Charles Griffin was partially funded by an NSERC Undergraduate Summer Research Award. The authors thank Nam Q. Le and an anonymous referee for some helpful remarks.