Article contents
Addition Theorems and Binary Expansions
Published online by Cambridge University Press: 20 November 2018
Abstract
Let an interval I ⊂ ℝ and subsets D 0, D 1 ⊂ I with D 0 ∪ D 1 = I and D 0 ∩ D 1 = Ø be given, as well as functions r 0: D 0 → I, r 1: D 1 → I. We investigate the system (S) of two functional equations for an unknown function f: I → [0, 1]: 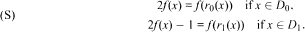 We derive conditions for the existence, continuity and monotonicity of a solution. It turns out that the binary expansion of a solution can be computed in a simple recursive way. This recursion is algebraic for, e.g., inverse trigonometric functions, but also for the elliptic integral of the first kind. Moreover, we use (S) to construct two kinds of peculiar functions: surjective functions whose intervals of constancy are residual in I, and strictly increasing functions whose derivative is 0 almost everywhere.
We derive conditions for the existence, continuity and monotonicity of a solution. It turns out that the binary expansion of a solution can be computed in a simple recursive way. This recursion is algebraic for, e.g., inverse trigonometric functions, but also for the elliptic integral of the first kind. Moreover, we use (S) to construct two kinds of peculiar functions: surjective functions whose intervals of constancy are residual in I, and strictly increasing functions whose derivative is 0 almost everywhere.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1995
References
- 6
- Cited by

