Hostname: page-component-cb9f654ff-lqqdg Total loading time: 0 Render date: 2025-08-30T02:23:09.767Z Has data issue: false hasContentIssue false
  • English
  • Français

Shortest paths in arbitrary plane domains

Part of: Real and complex geometry Special properties

Published online by Cambridge University Press:  09 November 2020

L. C. Hoehn ,
L. G. Oversteegen  and
E. D. Tymchatyn
L. C. Hoehn
Affiliation:
Department of Computer Science & Mathematics, Nipissing University, 100 College Drive, Box 5002, North Bay, ON P1B 8L7, Canada e-mail: loganh@nipissingu.ca
L. G. Oversteegen*
Affiliation:
Department of Mathematics, University of Alabama at Birmingham, Birmingham, AL 35294, USA
E. D. Tymchatyn
Affiliation:
Department of Mathematics and Statistics, University of Saskatchewan, 106 Wiggins Road, Saskatoon, SK S7N 5E6, Canada e-mail: tymchat@math.usask.ca
*
e-mail: overstee@uab.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $\Omega $ be a connected open set in the plane and 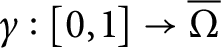$\gamma : [0,1] \to \overline {\Omega }$ a path such that 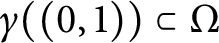$\gamma ((0,1)) \subset \Omega $. We show that the path 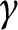$\gamma $ can be “pulled tight” to a unique shortest path which is homotopic to 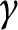$\gamma $, via a homotopy h with endpoints fixed whose intermediate paths 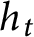$h_t$, for 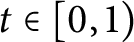$t \in [0,1)$, satisfy 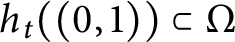$h_t((0,1)) \subset \Omega $. We prove this result even in the case when there is no path of finite Euclidean length homotopic to 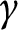$\gamma $ under such a homotopy. For this purpose, we offer three other natural, equivalent notions of a “shortest” path. This work generalizes previous results for simply connected domains with simple closed curve boundaries.

Keywords

Pathlengthshortestplane domainhomotopyanalytic covering map

MSC classification

Primary: 54F50: Spaces of dimension $leq 1$; curves, dendrites
Secondary: 51M25: Length, area and volume

Information

Type
Article
Information
Canadian Journal of Mathematics , Volume 74 , Issue 2 , April 2022 , pp. 349 - 367
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

L.C.H. was partially supported by NSERC grant RGPIN 435518. L.G.O. was partially supported by NSF-DMS-1807558. E.D.T. was partially supported by NSERC grant OGP-0005616.

References

Ahlfors, L. V., Conformal invariants: topics in geometric function theory. McGraw-Hill Series in Higher Mathematics, McGraw-Hill Book Co., New York, Düsseldorf, Johannesburg, 1973. MR 0357743.Google Scholar
Bourgin, R. D. and Renz, P. L., Shortest paths in simply connected regions in R2 . Adv. Math. 76(1989), no. 2, 260–295. MR 1013673.CrossRefGoogle Scholar
Cannon, J. W., Conner, G. R., and Zastrow, A., One-dimensional sets and planar sets are aspherical . Topol. Appl. 120(2002), nos. 1–2, 23–45. In memory of T. Benny Rushing. MR 1895481.CrossRefGoogle Scholar
Conway, J. B., Functions of one complex variable. II . Graduate Texts in Mathematics, 159, Springer-Verlag, New York, NY, 1995. MR 1344449.Google Scholar
Fatou, P., Séries trigonométriques et séries de Taylor . Acta Math. 30(1906), no. 1, 335–400. MR 1555035.CrossRefGoogle Scholar
Hoehn, L. C., Oversteegen, L. G., and Tymchatyn, E. D., Extension of isotopies in the plane . Trans. Amer. Math. Soc. 372(2019), no. 7, 4889–4915. MR 4009398.CrossRefGoogle Scholar
Hoehn, L. C., Oversteegen, L. G., and Tymchatyn, E. D., A canonical parameterization of paths in ℝ n . Houston J. Math. 46(2020), 465–489.Google Scholar
Kent, C., Homotopy type of planar continua. Preprint, 2020, arXiv:1709.09211 CrossRefGoogle Scholar
Kuratowski, K., Topology, Vol. II . New ed., revised and augmented. Translated from the French by A. Kirkor. Academic Press, New York, NY, 1968.Google Scholar
Lindelöf, E., Sur un principe générale de l’analyse et ses applications à la théorie de la représentation conforme . Acta Soc. Sci. Fennicae 46(1915), 1–35.Google Scholar
Morse, M., A special parameterization of curves . Bull. Amer. Math. Soc. 42(1936), no. 12, 915–922. MR 1563464.CrossRefGoogle Scholar
Pommerenke, C., Boundary behaviour of conformal maps . Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 299, Springer-Verlag, Berlin, Germany, 1992. MR 1217706.Google Scholar
Riesz, F., Über die Randwerte einer analytischen Funktion . Math. Z. 18(1923), no. 1, 87–95. MR 1544621.CrossRefGoogle Scholar
Riesz, F. and Riesz, M., Über die Randwerte einer analytischen Function 4. Cong. Scand. Math. Stockholm 1916, pp. 87–95.Google Scholar
Silverman, E., Equicontinuity and n-length . Proc. Amer. Math. Soc. 20(1969), 483–486. MR 0237719 (38 #6000).Google Scholar