Hostname: page-component-5b777bbd6c-rbv74 Total loading time: 0 Render date: 2025-06-18T17:37:31.791Z Has data issue: false hasContentIssue false
  • English
  • Français

The local converse theorem for quasi-split 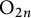$\mathrm {O}_{2n}$ and 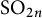$\mathrm {SO}_{2n}$

Part of: Lie groups Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  07 April 2025

Jaeho Haan Open the ORCID record for Jaeho Haan [Opens in a new window] ,
Yeansu Kim Open the ORCID record for Yeansu Kim [Opens in a new window]  and
Sanghoon Kwon Open the ORCID record for Sanghoon Kwon [Opens in a new window]
Jaeho Haan
Affiliation:
Department of Mathematics Education, Catholic Kwandong University, Gangneung, South Korea e-mail: jaehohaan@gmail.com skwon@cku.ac.kr
Yeansu Kim*
Affiliation:
Department of Mathematics Education, Chonnam National University, Gwangju, South Korea
Sanghoon Kwon
Affiliation:
Department of Mathematics Education, Catholic Kwandong University, Gangneung, South Korea e-mail: jaehohaan@gmail.com skwon@cku.ac.kr
*
e-mail: ykim@jnu.ac.kr
Get access Rights & Permissions [Opens in a new window]

Abstract

Let F be a non-archimedean local field of characteristic not equal to 2. In this article, we prove the local converse theorem for quasi-split 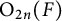$\mathrm {O}_{2n}(F)$ and 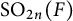$\mathrm {SO}_{2n}(F)$, via the description of the local theta correspondence between 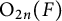$\mathrm {O}_{2n}(F)$ and 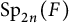$\mathrm {Sp}_{2n}(F)$. More precisely, as a main step, we explicitly describe the precise behavior of the 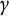$\gamma $-factors under the correspondence. Furthermore, we apply our results to prove the weak rigidity theorems for irreducible generic cuspidal automorphic representations of 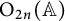$\mathrm {O}_{2n}(\mathbb {A})$ and 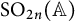$\mathrm {SO}_{2n}(\mathbb {A})$, respectively, where 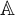$\mathbb {A}$ is a ring of adele of a global number field L.

Keywords

Gamma factorseven orthogonal groupslocal converse theoremtheta correspondence

MSC classification

Primary: 11F70: Representation-theoretic methods; automorphic representations over local and global fields 22E50: Representations of Lie and linear algebraic groups over local fields
Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 38
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

J. H. has been supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. 2020R1F1A1A01048645). Y. K. has been supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIP) (No. RS-2022-0016551 and No. RS-2024-00415601 (G-BRL)) and by Chonnam National University (Grant number: 2022-0123). J. H. and S. K. have been supported by NRF grant (No. RS-2023-00237811).

References

Adams, J. and Barbasch, D. M., Reductive dual pair correspondence for complex groups . J. Funct. Anal. 132(1995), 1–42.Google Scholar
Arthur, J., The endoscopic classification of representations. Orthogonal and symplectic groups . Amer. Math. Soc. Colloq. Publ. 61(2013), 590 pp.Google Scholar
Atobe, H., On the uniqueness of generic representations in an $L$ -packet . Int. Math. Res. Not. IMRN 23(2017), 7051–7068.Google Scholar
Atobe, H., The local theta correspondence and the local Gan–Gross–Prasad conjecture for the symplectic-metaplectic case . Math. Ann. 371(2018), 225–295.Google Scholar
Atobe, H. and Gan, W. T., On the local Langlands correspondence and Arthur conjecture for even orthogonal groups . Represent. Theory 21(2017), 354–415.Google Scholar
Ban, D. and Jantzen, C., The Langlands classification for non-connected $p$ -adic groups . Israel J. Math. 126(2001), 239–261.Google Scholar
Ban, D. and Jantzen, C., Degenerate principal series for even-orthogonal groups . Represent. Theory 7(2003), 440–480.Google Scholar
Bernstein, J. H. and Zelevinskii, A. V., Representations of the group GL(n,F) where F is a non-Archimedean local field . Russian Math. Surv. 31(1976), no. 3, 1–68.Google Scholar
Cai, Y., Friedberg, S., and Kaplan, E., The generalized doubling method: Local theory . Geom. Funct. Anal. 32(2022), 1233–1333.Google Scholar
Casselman, W. and Shahidi, F., On irreducibility of standard modules for generic representations . Ann. Sci. École Norm. Sup. 31(1998), 561–589.Google Scholar
Castillo, H., Langlands functoriality conjecture for ${SO}_{2n}^{\ast }$ in positive characteristic. Preprint, arXiv:2201.03119v1Google Scholar
Castillo, H., Henniart, G., and Lomelí, L., On generic representations of quasi-split reductive groups over local fields of positive characteristic. Preprint, arXiv:2412.00229v1 Google Scholar
Chai, J., Bessel functions and local converse conjecture of Jacquet . J. Eur. Math. Soc. 21(2019), no. 6, 1703–1728.Google Scholar
Cogdell, J. W., Kim, H., Piathtski-Shapiro, I. I., and Shahidi, F., On lifting from classical groups to $GL(n)$ . Publ. Math. Inst. Hautes Études Sci 93(2001), 5–30.Google Scholar
Cogdell, J. W., Piatetski-Shapiro, I. I., and Shahidi, F., Functoriality for the quasisplit classical groups . In: J. Arthur, J. W. Cogdell, S. Gelbart, D. Goldberg, D. Ramakrishnan, and J. Yu (eds.), On certain L-functions, Clay Mathematics Proceedings, American Mathematical Society, Providence, RI, 2011, pp. 117–140.Google Scholar
Cogdell, J. W., Shahidi, F., and Tsai, T.-L., Local Langlands correspondence for ${GL}_n$ and the exterior and symmetric square $\varepsilon$ -factors . Duke Math. J. 166(2017) no. 11, 2053–2132.Google Scholar
Gan, W. T., Gross, B., and Prasad, D., Symplectic local root numbers, central critical $L$ values, and restriction problems in the representation theory of classical groups . Astérisque 346(2012), 1–109.Google Scholar
Gan, W. T. and Ichino, A., Formal degrees and local theta correspondence . Invent. Math. 195(2014) no. 3, 509–672.Google Scholar
Gan, W. T. and Lomelí, L., Globalization of supercuspidal representations over function fields and applications . J. Eur. Math. Soc. 20(2018), no. 11, 2813–2858.Google Scholar
Gan, W. T. and Savin, G., Representations of metaplectic groups $I$ : epsilon dichotomy and local Langlands correspondence . Compos. Math. 148(2012), 1655–1694.Google Scholar
Gan, W. T. and Takeda, S., On the Howe duality conjecture in classical theta correspondence . In: D. Jiang, F. Shahidi, and D. Soudry (eds.), Advances in the theory of automorphic forms and their $L$ -functions, Contemporary Mathematics, 664, American Mathematical Society, Providence, RI, 2016, pp. 105–117.Google Scholar
Gan, W. T. and Takeda, S., A proof of the Howe duality conjecture . J. Amer. Math. Soc. 29(2016), no. 2, 473–493.Google Scholar
Ginzberg, D., Rallis, S., and Soudry, D., Periods, poles of $L$ -functions and symplectic-orthogonal theta lifts . J. Reine Angew. Math. 487(1997), 85–114.Google Scholar
Haan, J., A local converse theorem for ${\overset{\sim }{Sp}}_{2n}$ : The generic case. Preprint, arXiv:2212.05234 Google Scholar
Hazeltine, A., On the local converse theorem for quasi-split $S{O}_{2n}$ . Preprint, 2022.Google Scholar
Hazeltine, A. and Liu, B., On the local converse theorem for split $S{O}_{2l}$ . Represent. Theory 29(2025), 209–255.Google Scholar
Heiermann, V. and Opdam, E., On the tempered L-functions conjecture . Amer. J. Math. 135(2013), no. 3, 777–799.Google Scholar
Henniart, G., Caractérisation de la correspondance de Langlands locale par les facteurse de paires . Invent. Math. 113(1993), 339–350.Google Scholar
Jacquet, H. and Liu, B., On the local converse theorem for $p$ -adic ${GL}_n$ . Amer. J. Math. 140(2018), no. 5, 1399–1422.Google Scholar
Jacquet, H., Piatetski-Shapiro, I. I., and Shalika, J. A., Rankin–Selberg convolutions . Amer. J. Math. 105(1983), 367–464.Google Scholar
Jacquet, H. and Shalika, J. A., Rankin–Selberg convolutions: Archimedean theory . In: S. Gelbart, R. Howe, and P. Sarnak (eds.), Festschrift in honor of I. I. Piatetski-Shapiro on the occasion of his sixtieth birthday. Part I (Ramat Aviv, 1989), Israel Mathematical Conference Proceedings, 2, Weizmann, Jerusalem, 1990, 125–207.Google Scholar
Jiang, D., On local $\gamma$ -factors. In: Weng, L. and Nakamura, I. (eds.), Arithmetic geometry and number theory, Series on Number Theory and its Applications, 1, World Scientific Publishing, Hackensack, NJ, 2006, pp. 1–28.Google Scholar
Jiang, D. and Soudry, D., The local converse theorem for $SO\left(2n+1\right)$ and applications . Ann. Math. (2) 157(2003) no.3, 743–806.Google Scholar
Jo, Y., The local converse theorem for odd special orthogonal and symplectic groups in positive characteristic. Preprint, arXiv:2205.09004 Google Scholar
Kaplan, E., Complementary results on the Rankin-Selberg gamma factors of classical groups . J. Number Theory 146(2015), 390–447.Google Scholar
Kim, H., Automorphic  $L$ -functions. In: J. W. Cogdell, H. Kim, and M. Murty (eds.), Lectures on automorphic L-functions, Fields Institute Monograph, 20, American Mathematical Society, Providence, RI (2004), pp. 97–201.Google Scholar
Kudla, S. S., Notes on the local theta correspondence, unpublished notes, 1996. Available at: http://www.math.utoronto.ca/skudla/castle.pdf.Google Scholar
Lapid, E. M. and Rallis, S., On the local factors of representations of classical groups . In: Cogdell, J. W., Jiang, D., Kudla, S. S., Soudry, D., and Stanton, R. (eds.), Automorphic representations, $L$ -functions and applications: Progress and prospects, Ohio State University Mathematical Research Institute Publications, 11, de Gruyter, Berlin, 2005, 309–359.Google Scholar
Lomeli, L., The LS method for the classical groups in positive characteristic and the Riemann hypothesis . Amer. J. Math. 137(2015), no. 2, 473–496.Google Scholar
Lomeli, L., The Langlands-Shahidi method over function fields: Ramanujan Conjecture and Riemann Hypothesis for the unitary groups. Preprint, arXiv:1507.03625 Google Scholar
Morimoto, K., On the irreducibility of global descents for even unitary groups and its applications . Trans. Amer. Math. Soc. 370(2018), 6245–6295.Google Scholar
Muić, G. and Savin, G., Symplectic-orthogonal theta lifts of generic descrete series . Duke Math. J. 101(2000), 317–333.Google Scholar
Rallis, S., On the Howe duality conjecture . Compos. Math. 51(1984), no. 3, 333–399.Google Scholar
Shahidi, F., A proof of Langlands’ conjecture on Plancherel measures; complementary series for $p$ -adic groups . Ann. Math. 132(1990), no. 2, 273–330.Google Scholar
Waldspurger, J.-L., Démonstration d’une conjecture de dualité de Howe dans le cas $p$ -adique, $p\ne 2$ . In: S. Gelbart, R. Howe, and P. Sarnak (eds.), Festschrift in honor of I. I. Piatetski-Shapiro on the occasion of his sixtieth birthday, Part I (Ramat Aviv, 1989), Israel Mathematical Conference Proceedings, 2, Weizmann, Jerusalem, 1990, pp. 267–324. (French).Google Scholar
Yan, P. and Zhang, Q., On a refined local converse theorem for $SO(4)$ . Proc. Amer. Math. Soc. 152(2024), 4959–4976.Google Scholar
Yan, P. and Zhang, Q., Product of Rankin-Selberg convolutions and a new proof of Jacquet’s local converse conjecture. Preprint, arXiv:2309.10445 Google Scholar
Zhang, Q., A local converse theorem for ${Sp}_{2r}$ . Math. Ann. 372(2018), nos. 1–2, 451–488.Google Scholar
Zhang, Q., A local converse theorem for ${U}_{2r+1}$ . Trans. Amer. Math. Soc. 371(2019), no. 8, 5631–5654.Google Scholar