Published online by Cambridge University Press: 07 August 2020
Given an action 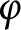 ${\varphi }$
of inverse semigroup S on a ring A (with domain of
${\varphi }$
of inverse semigroup S on a ring A (with domain of 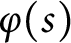 ${\varphi }(s)$
denoted by
${\varphi }(s)$
denoted by 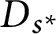 $D_{s^*}$
), we show that if the ideals
$D_{s^*}$
), we show that if the ideals 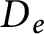 $D_e$
, with e an idempotent, are unital, then the skew inverse semigroup ring
$D_e$
, with e an idempotent, are unital, then the skew inverse semigroup ring 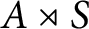 $A\rtimes S$
can be realized as the convolution algebra of an ample groupoid with coefficients in a sheaf of (unital) rings. Conversely, we show that the convolution algebra of an ample groupoid with coefficients in a sheaf of rings is isomorphic to a skew inverse semigroup ring of this sort. We recover known results in the literature for Steinberg algebras over a field as special cases.
$A\rtimes S$
can be realized as the convolution algebra of an ample groupoid with coefficients in a sheaf of (unital) rings. Conversely, we show that the convolution algebra of an ample groupoid with coefficients in a sheaf of rings is isomorphic to a skew inverse semigroup ring of this sort. We recover known results in the literature for Steinberg algebras over a field as special cases.
B. S. thanks the Fulbright commission for its support in visiting the Federal University of Santa Catarina in Brazil and the PSC-CUNY. D. G. was partially supported by Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) grant numbers 304487/2017-1 and 406122/2018-0 and Capes-PrInt grant number 88881.310538/2018-01—Brazil.