Hostname: page-component-cb9f654ff-r5d9c Total loading time: 0 Render date: 2025-08-27T22:46:15.312Z Has data issue: false hasContentIssue false
  • English
  • Français

(0, 2) – Interpolation of Entire Functions

Published online by Cambridge University Press:  20 November 2018

R. Gervais ,
Q. I. Rahman  and
G. Schmeisser
R. Gervais
Affiliation:
Université de Montréal, Montréal, Québec
Q. I. Rahman
Affiliation:
Université de Montréal, Montréal, Québec
G. Schmeisser
Affiliation:
Universität Erlangen-Nürnberg, Erlangen, West Germany
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a triangular matrix A whose n th row consists of the n points

(1.1)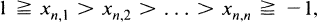

Turán et al. ([12], [1], [2], [3]) considered the problem of existence, uniqueness, representation, convergence, etc. of polynomials f 2n – 1 of degree ≧2n – 1 where the values of f 2n – 1 and those of its second derivative are prescribed at the points (1.1), i.e.,

(1.2)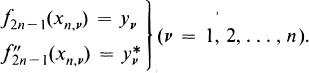

The choice of the points (1.1) is important. They found the zeros

(1.3)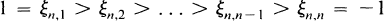

of the polynomial

(1.1)

where P n – 1 is the (n − 1) Legendre polynomial with the normalization P n – 1(l) = 1 to be the most convenient.

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 38 , Issue 5 , 01 October 1986 , pp. 1210 - 1227
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Balázs, J. and Turán, P., Notes on interpolation. II. (Explicit formulae), Acta Math. Acad. Sci. Hung. 8 (1957), 201–215.Google Scholar
2. Balázs, J. and Turán, P., Notes on interpolation. III. (Convergence), Acta Math. Acad. Sci. Hung. 9 (1958), 195–214.Google Scholar
3. Balázs, J. and Turán, P., Notes on interpolation. IV. (Inequalities), Acta Math. Acad. Sci. Hung. 9 (1958), 243–258.Google Scholar
4. Boas, R. P. Jr., Entire functions (Academic Press, New York, 1954).Google Scholar
5. Gervais, R. and Rahman, Q. I., An extension of Carlson's theorem for entire functions of exponential type, Trans. Amer. Math. Soc. 235 (1978), 387–394.Google Scholar
6. Gervais, R. and Rahman, Q. I., An extension of Carlson's theorem for entire functions of exponential type. II, J. Math. Anal. Appl. 69 (1979), 585–602.Google Scholar
7. Gervais, R., Rahman, Q. I. and Schmeisser, G., Simultaneous interpolation and approximation by entire functions of exponential type, Numerische Methoden der Approximations theorie, Band 4, ISNM 42 (Birkhauser-Verlag, Basel, 1978), 145–153.Google Scholar
8. Gervais, R., Rahman, Q. I. and Schmeisser, G., Simultaneous interpolation and approximation, In Polynomial and spline approximation (D. Reidel Publ. Comp., Dordrecht-Boston, 1979), 203–223.Google Scholar
9. Gervais, R., Rahman, Q. I. and Schmeisser, G., Approximation by (0, 2)-interpolating entire functions of exponential type, J. Math. Anal. Appl. 82 (1981), 184–199.Google Scholar
10. Kiš, O., On trigonometric interpolation (Russian), Acta Math. Acad. Sci. Hung. 11 (1960), 255–276.Google Scholar
11. Sharma, A. and Varma, A. K., Trigonometric interpolation, Duke Math. J. 32 (1965), 341–358.Google Scholar
12. Surányi, J. and Turän, P., Notes on interpolation. I. (On some interpolatorical properties of the ultraspherical polynomials), Acta Math. Acad. Sci. Hung. 6 (1955), 67–79.Google Scholar