Contents
Research Article
Non differentiable symmetric duality
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 177-188
-
- Article
-
- You have access
- Export citation
Sign pattern matrices that allow a nilpotent matrix
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 189-196
-
- Article
-
- You have access
- Export citation
The existence of bounded harmonic functions on C-H manifolds
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 197-207
-
- Article
-
- You have access
- Export citation
A note on Hall closure of metanilpotent fitting classes
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 209-212
-
- Article
-
- You have access
- Export citation
A selection theorem for weak upper semi-continuous set-valued mappings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 213-227
-
- Article
-
- You have access
- Export citation
A continuous analogue and an extension of Radó's formulæ
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 229-233
-
- Article
-
- You have access
- Export citation
Semilinear problems on the half space with a hole
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 235-247
-
- Article
-
- You have access
- Export citation
Modules arising from some relative injectives
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 249-260
-
- Article
-
- You have access
- Export citation
Essential covers and complements of radicals
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 261-266
-
- Article
-
- You have access
- Export citation
Set covering number for a finite set
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 267-269
-
- Article
-
- You have access
- Export citation
A note on strong geometric isolation in 3-orbitfolds
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 271-280
-
- Article
-
- You have access
- Export citation
Diophantine equations of Erdös-Moser type
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 281-292
-
- Article
-
- You have access
- Export citation
A note on frame starters
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 293-297
-
- Article
-
- You have access
- Export citation
On squares of Jacobson radical rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 299-303
-
- Article
-
- You have access
- Export citation
Global attractivity and stability in some monotone discrete dynamical systems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 305-324
-
- Article
-
- You have access
- Export citation
Recycling circle planes
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 325-340
-
- Article
-
- You have access
- Export citation
Algorithmes des fractions continues et de Jacobi-Perron
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 341-350
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian Ph.D. Theses
E-varieties and E-pseudovarieties of regular semigroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 351-352
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 53 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 53 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

 of the equation −Δ
of the equation −Δ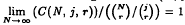 was proved by Rödl, no nontrivial upper bound for
was proved by Rödl, no nontrivial upper bound for 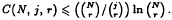
 . For
. For 