Contents
Research Article
Abelian Groups that are unions of proper subgroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 1-7
-
- Article
-
- You have access
- Export citation
Convolution properties of a class of bounded analytic functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 9-23
-
- Article
-
- You have access
- Export citation
A nonlinear ergodic theorem for asymptotically nonexpansive mappings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 25-36
-
- Article
-
- You have access
- Export citation
A formula on the approximate subdifferential of the difference of convex functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 37-41
-
- Article
-
- You have access
- Export citation
On the duality of some martingale spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 43-52
-
- Article
-
- You have access
- Export citation
Conical inverse mapping theorems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 53-60
-
- Article
-
- You have access
- Export citation
Semiregular group divisible designs with dual properties
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 61-69
-
- Article
-
- You have access
- Export citation
Some nilpotent Lie algebras of even dimension
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 71-77
-
- Article
-
- You have access
- Export citation
Structurally stable flows
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 79-90
-
- Article
-
- You have access
- Export citation
Rings whose additive endomorphisms are ring endomorphisms
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 91-103
-
- Article
-
- You have access
- Export citation
A property of analytic functions with Hadamard gaps
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 105-112
-
- Article
-
- You have access
- Export citation
On the dynamics of a periodic delay logistic equation with diffusion
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 113-134
-
- Article
-
- You have access
- Export citation
Dichotomies for systems with discontinuous coefficients
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 135-141
-
- Article
-
- You have access
- Export citation
A note on the radial growth of Bloch functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 143-149
-
- Article
-
- You have access
- Export citation
A note on high degree linear complementarity problems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 151-155
-
- Article
-
- You have access
- Export citation
On the Pass-equivalence of links
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 157-162
-
- Article
-
- You have access
- Export citation
On a conjecture of Z. Jianzhong
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 163-170
-
- Article
-
- You have access
- Export citation
The Weak* Karlovitz lemma for dual lattices
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 171-176
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 45 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 45 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
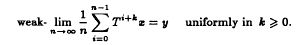
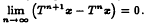 . We also present a weak convergence theorem for asymptotically nonexpansive semigroups.
. We also present a weak convergence theorem for asymptotically nonexpansive semigroups.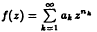 satisfying
satisfying 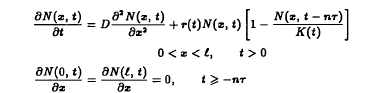
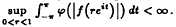 The subclass
The subclass 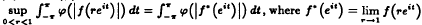 for almost all points
for almost all points