Contents
Research Article
Necessary and sufficient conditions for oscillations of delay differential inequalities
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 161-165
-
- Article
-
- You have access
- Export citation
On a subclass of Bazilevic functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 167-170
-
- Article
-
- You have access
- Export citation
On near-rings in which the constants form an ideal
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 171-175
-
- Article
-
- You have access
- Export citation
A class of strongly degenerate elliptic operators
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 177-200
-
- Article
-
- You have access
- Export citation
Strong convergence of selections implied by weak
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 201-214
-
- Article
-
- You have access
- Export citation
Global dimensions of right coherent rings with left Krull dimension
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 215-223
-
- Article
-
- You have access
- Export citation
A variational-like inequality problem
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 225-231
-
- Article
-
- You have access
- Export citation
Nearest points to closed sets and directional derivatives of distance functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 233-238
-
- Article
-
- You have access
- Export citation
An existence theorem for an optimal control problem in banach spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 239-247
-
- Article
-
- You have access
- Export citation
Character degrees and CLT-groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 249-254
-
- Article
-
- You have access
- Export citation
A note on subnormal defect in finite soluble groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 255-258
-
- Article
-
- You have access
- Export citation
Every chaotic interval map has a scrambled set in the recurrent set
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 259-264
-
- Article
-
- You have access
- Export citation
Graph varieties containing Murskii's groupoid
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 265-276
-
- Article
-
- You have access
- Export citation
Epicomplete archimedean lattice-ordered groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 277-286
-
- Article
-
- You have access
- Export citation
Generalised convexity and duality in multiple objective programming
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 287-299
-
- Article
-
- You have access
- Export citation
Elementary observations on 2-categorical limits
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 301-317
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian Ph.D. theses
Distance-regular antipodal covering graphs
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 319-320
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 39 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 39 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
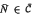 such that every
such that every 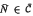 . It turns out that near-rings
. It turns out that near-rings 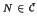 have an ideal structure which is similar to the ideal structure of abstract affine near-rings, in contrast to the situation for arbitrary elements of
have an ideal structure which is similar to the ideal structure of abstract affine near-rings, in contrast to the situation for arbitrary elements of 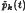 the projection of
the projection of 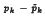 converges weakly to zero then
converges weakly to zero then 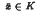 ε
ε