Contents
Research Article
On subparacompact and countably subparacompact spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 289-304
-
- Article
-
- You have access
- Export citation
Exact variational representations for the solution of the simple parabolic equation
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 305-314
-
- Article
-
- You have access
- Export citation
On the analyticity of generalized minimal surfaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 315-320
-
- Article
-
- You have access
- Export citation
Some definitions of finiteness
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 321-330
-
- Article
-
- You have access
- Export citation
Minimal vector lattice covers
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 331-335
-
- Article
-
- You have access
- Export citation
Block idempotents and the Brauer correspondence
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 337-340
-
- Article
-
- You have access
- Export citation
A problem of Hanna Neumann on closed sets of group words
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 341-342
-
- Article
-
- You have access
- Export citation
On a sequence of Fourier coefficients
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 343-349
-
- Article
-
- You have access
- Export citation
The log log law for multidimensional stochastic integrals and diffusion processes
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 351-356
-
- Article
-
- You have access
- Export citation
On a class of power-associative periodic rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 357-362
-
- Article
-
- You have access
- Export citation
Coretraction-fibrations are retractions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 363-374
-
- Article
-
- You have access
- Export citation
On finite soluble groups and the fixed-point groups of automorphisms
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 375-378
-
- Article
-
- You have access
- Export citation
Third Engel groups and the Macdonald-Neumann conjecture
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 379-386
-
- Article
-
- You have access
- Export citation
The weak density of the non-invertible elements of a commutative algebra
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 387-390
-
- Article
-
- You have access
- Export citation
Varieties of soluble groups and a dichotomy of P. Hall
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 391-410
-
- Article
-
- You have access
- Export citation
Remark on ordered abelian groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 411-413
-
- Article
-
- You have access
- Export citation
An elementary existence theorem for entire functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 415-419
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian Ph.D. theses
Superlinear variational boundary value problems and nonuniqueness
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 421-422
-
- Article
-
- You have access
- Export citation
Abelian Rickart semirings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 423-424
-
- Article
-
- You have access
- Export citation
Filtrations and valuations on rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 425-426
-
- Article
-
- You have access
- Export citation
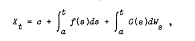

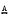 denote the variety of all abelian groups and, for each prime p, let
denote the variety of all abelian groups and, for each prime p, let 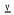 be a subvariety of a product of (finitely many) varieties each of which is either soluble or Cross.
be a subvariety of a product of (finitely many) varieties each of which is either soluble or Cross.