Contents
Research Article
Multipliers between some function spaces on groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 1-11
-
- Article
-
- You have access
- Export citation
A martingale central limit theorem without negligibility conditions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 13-19
-
- Article
-
- You have access
- Export citation
A new graph product and its spectrum
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 21-28
-
- Article
-
- You have access
- Export citation
Asymptotics applied to nonlinear boundary-value problems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 29-35
-
- Article
-
- You have access
- Export citation
Differentiable retracts and a modified inverse function theorem
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 37-43
-
- Article
-
- You have access
- Export citation
Normal and invertible composition operators
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 45-54
-
- Article
-
- You have access
- Export citation
Oscillation theorems for semilinear hyperbolic and ultrahyperbolic operators
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 55-64
-
- Article
-
- You have access
- Export citation
Duality in finite dimensional complex space
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 65-75
-
- Article
-
- You have access
- Export citation
Monotone operators and dentability
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 77-82
-
- Article
-
- You have access
- Export citation
Estimation of the integral of a stochastic process
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 83-93
-
- Article
-
- You have access
- Export citation
A functorial version of a construction of Hochschild and Mostow for representations of Lie algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 95-98
-
- Article
-
- You have access
- Export citation
On coinduced corepresentations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 99-103
-
- Article
-
- You have access
- Export citation
Characterisation of normed linear spaces with Mazur's intersection property
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 105-123
-
- Article
-
- You have access
- Export citation
On characterisation of finitary algebraic categories
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 125-135
-
- Article
-
- You have access
- Export citation
An analogue of Banach's contraction principle for 2-metric spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 137-143
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD theses
On multifunctions and multimeasures
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 145-146
-
- Article
-
- You have access
- Export citation
Analytic extension of riemannian manifolds
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 147-148
-
- Article
-
- You have access
- Export citation
Lacunary sets for connected and totally disconnected compact groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 149-151
-
- Article
-
- You have access
- Export citation
Tight Riesz orders via congruences
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 153-154
-
- Article
-
- You have access
- Export citation
Some topics in the theory of ring structures on abelian groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 155-156
-
- Article
-
- You have access
- Export citation
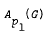 and multipliers of
and multipliers of 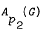 are different, provided
are different, provided 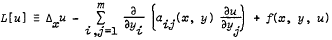
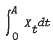 . This design question is shown to be directly related to finding sampling points of
. This design question is shown to be directly related to finding sampling points of  be a Lie algebra,
be a Lie algebra, 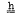 a complemented ideal of
a complemented ideal of