No CrossRef data available.
Article contents
Variational formulation of higher order elliptic boundary value problems
Published online by Cambridge University Press: 17 April 2009
Abstract
Let A be an elliptic (partial) differential operator of order 2m on a compact manifold 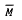 with boundary Г. Let B be a normal system of m differential boundary operators on Г. Assume all manifolds and coefficients are arbitrarily smooth. We construct sesquilinear forms J in terms of which there are equivalent variational formulations of the natural boundary value problems determined by A and B with solutions in Sobolev spaces HS (M), 0 < s < 2m. Such forms are also constructed for problems with mixed boundary conditions. The variational formulation permits localization of a priori estimates and the interchange of existence and uniqueness questions between the boundary value problem and an associated adjoint problem.
with boundary Г. Let B be a normal system of m differential boundary operators on Г. Assume all manifolds and coefficients are arbitrarily smooth. We construct sesquilinear forms J in terms of which there are equivalent variational formulations of the natural boundary value problems determined by A and B with solutions in Sobolev spaces HS (M), 0 < s < 2m. Such forms are also constructed for problems with mixed boundary conditions. The variational formulation permits localization of a priori estimates and the interchange of existence and uniqueness questions between the boundary value problem and an associated adjoint problem.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1983

