No CrossRef data available.
Article contents
TWO PROBLEMS CONCERNING IRREDUCIBLE ELEMENTS IN RINGS OF INTEGERS OF NUMBER FIELDS
Published online by Cambridge University Press: 02 March 2017
Abstract
Let 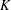 $K$ be a number field with ring of integers
$K$ be a number field with ring of integers 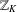 $\mathbb{Z}_{K}$ . We prove two asymptotic formulas connected with the distribution of irreducible elements in
$\mathbb{Z}_{K}$ . We prove two asymptotic formulas connected with the distribution of irreducible elements in 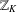 $\mathbb{Z}_{K}$ . First, we estimate the maximum number of nonassociated irreducibles dividing a nonzero element of
$\mathbb{Z}_{K}$ . First, we estimate the maximum number of nonassociated irreducibles dividing a nonzero element of 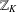 $\mathbb{Z}_{K}$ of norm not exceeding
$\mathbb{Z}_{K}$ of norm not exceeding  $x$ (in absolute value), as
$x$ (in absolute value), as 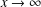 $x\rightarrow \infty$ . Second, we count the number of irreducible elements of
$x\rightarrow \infty$ . Second, we count the number of irreducible elements of 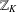 $\mathbb{Z}_{K}$ of norm not exceeding
$\mathbb{Z}_{K}$ of norm not exceeding  $x$ lying in a given arithmetic progression (again, as
$x$ lying in a given arithmetic progression (again, as 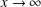 $x\rightarrow \infty$ ). When
$x\rightarrow \infty$ ). When 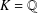 $K=\mathbb{Q}$ , both results are classical; a new feature in the general case is the influence of combinatorial properties of the class group of
$K=\mathbb{Q}$ , both results are classical; a new feature in the general case is the influence of combinatorial properties of the class group of 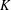 $K$ .
$K$ .
Information
- Type
- Research Article
- Information
- Copyright
- © 2017 Australian Mathematical Publishing Association Inc.
Footnotes
Research of the first author is supported by NSF award DMS-1402268.

