Article contents
SYMMETRIC ITINERARY SETS: ALGORITHMS AND NONLINEAR EXAMPLES
Published online by Cambridge University Press: 20 March 2019
Abstract
We describe how to approximate fractal transformations generated by a one-parameter family of dynamical systems 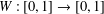 $W:[0,1]\rightarrow [0,1]$ constructed from a pair of monotone increasing diffeomorphisms
$W:[0,1]\rightarrow [0,1]$ constructed from a pair of monotone increasing diffeomorphisms 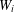 $W_{i}$ such that
$W_{i}$ such that 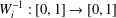 $W_{i}^{-1}:[0,1]\rightarrow [0,1]$ for
$W_{i}^{-1}:[0,1]\rightarrow [0,1]$ for 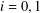 $i=0,1$. An algorithm is provided for determining the unique parameter value such that the closure of the symbolic attractor
$i=0,1$. An algorithm is provided for determining the unique parameter value such that the closure of the symbolic attractor 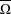 $\overline{\unicode[STIX]{x1D6FA}}$ is symmetrical. Several examples are given, one in which the
$\overline{\unicode[STIX]{x1D6FA}}$ is symmetrical. Several examples are given, one in which the 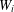 $W_{i}$ are affine and two in which the
$W_{i}$ are affine and two in which the 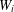 $W_{i}$ are nonlinear. Applications to digital imaging are also discussed.
$W_{i}$ are nonlinear. Applications to digital imaging are also discussed.
MSC classification
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 100 , Issue 1 , August 2019 , pp. 109 - 118
- Copyright
- © 2019 Australian Mathematical Publishing Association Inc.
Footnotes
The author acknowledges support from an Australian Research Council Discovery Project (project number DP160102021) funded by the Australian Government.
References
- 1
- Cited by

