Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yang, Quan-Hui
and
Chen, Yong-Gao
2015.
On the cardinality of general h-fold sumsets.
European Journal of Combinatorics,
Vol. 47,
Issue. ,
p.
103.
Yu, Wang-Xing
Chen, Yong-Gao
and
Chen, Shi-Qiang
2023.
On the restricted sumsets containing powers of an integer.
European Journal of Combinatorics,
Vol. 114,
Issue. ,
p.
103795.
Yu, Wang-Xing
and
Zhao, Jun-Jia
2026.
An optimal lower bound for the size of the restricted sumsets containing powers.
Journal of Number Theory,
Vol. 280,
Issue. ,
p.
785.

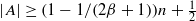 , then (
, then (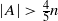 , then (
, then ( cannot be improved.
cannot be improved.