Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Maghsoudi, Saeid
2013.
The space of vector‐valued integrable functions under certain locally convex topologies.
Mathematische Nachrichten,
Vol. 286,
Issue. 2-3,
p.
260.
MAGHSOUDI, S.
and
SEOANE-SEPÚLVEDA, J. B.
2014.
HYPERGROUP ALGEBRAS AS TOPOLOGICAL ALGEBRAS.
Bulletin of the Australian Mathematical Society,
Vol. 90,
Issue. 3,
p.
486.
Samea, H.
and
Fasahat, E.
2017.
Strict topology on locally compact groups.
Topology and its Applications,
Vol. 226,
Issue. ,
p.
42.
Nowak, Marian
2020.
Discrete measures and strict topologies.
Topology and its Applications,
Vol. 269,
Issue. ,
p.
106923.

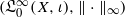 . Next, by showing that
. Next, by showing that 