No CrossRef data available.
Article contents
SPACES OF SPECIAL QUADRILATERALS
Published online by Cambridge University Press: 07 January 2019
Abstract
We describe the parameter spaces of some families of quadrilaterals, such as parallelograms, rectangles, rhombuses, cyclic quadrilaterals and trapezoids. For this purpose, we prove that the closed  $n$-disc
$n$-disc 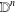 $\mathbb{D}^{n}$ is the unique topological
$\mathbb{D}^{n}$ is the unique topological  $n$-manifold (with boundary) whose boundary and interior are homeomorphic to
$n$-manifold (with boundary) whose boundary and interior are homeomorphic to 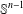 $\mathbb{S}^{n-1}$ and
$\mathbb{S}^{n-1}$ and 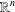 $\mathbb{R}^{n}$, respectively. Roughly speaking, our main result states that the natural compactifications of the parameter spaces of cyclic quadrilaterals and of trapezoids, modulo similarity, are both homeomorphic to
$\mathbb{R}^{n}$, respectively. Roughly speaking, our main result states that the natural compactifications of the parameter spaces of cyclic quadrilaterals and of trapezoids, modulo similarity, are both homeomorphic to 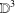 $\mathbb{D}^{3}$.
$\mathbb{D}^{3}$.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 100 , Issue 1 , August 2019 , pp. 155 - 167
- Copyright
- © 2019 Australian Mathematical Publishing Association Inc.
Footnotes
The first author is partially supported by CONACYT grant FORDECYT 265667; the second author is partially supported by funding from CIC-UMSNH.

