No CrossRef data available.
Article contents
A SHARP UPPER BOUND FOR THE SUM OF RECIPROCALS OF LEAST COMMON MULTIPLES II
Published online by Cambridge University Press: 09 June 2022
Abstract
Let n and k be positive integers with 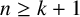 $n\ge k+1$ and let
$n\ge k+1$ and let 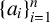 $\{a_i\}_{i=1}^n$ be a strictly increasing sequence of positive integers. Let
$\{a_i\}_{i=1}^n$ be a strictly increasing sequence of positive integers. Let 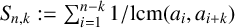 $S_{n, k}:=\sum _{i=1}^{n-k} {1}/{\mathrm {lcm}(a_{i},a_{i+k})}$. In 1978, Borwein [‘A sum of reciprocals of least common multiples’, Canad. Math. Bull. 20 (1978), 117–118] confirmed a conjecture of Erdős by showing that
$S_{n, k}:=\sum _{i=1}^{n-k} {1}/{\mathrm {lcm}(a_{i},a_{i+k})}$. In 1978, Borwein [‘A sum of reciprocals of least common multiples’, Canad. Math. Bull. 20 (1978), 117–118] confirmed a conjecture of Erdős by showing that 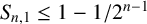 $S_{n,1}\le 1-{1}/{2^{n-1}}$. Hong [‘A sharp upper bound for the sum of reciprocals of least common multiples’, Acta Math. Hungar. 160 (2020), 360–375] improved Borwein’s upper bound to
$S_{n,1}\le 1-{1}/{2^{n-1}}$. Hong [‘A sharp upper bound for the sum of reciprocals of least common multiples’, Acta Math. Hungar. 160 (2020), 360–375] improved Borwein’s upper bound to 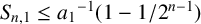 $S_{n,1}\le {a_{1}}^{-1}(1-{1}/{2^{n-1}})$ and derived optimal upper bounds for
$S_{n,1}\le {a_{1}}^{-1}(1-{1}/{2^{n-1}})$ and derived optimal upper bounds for 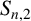 $S_{n,2}$ and
$S_{n,2}$ and 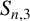 $S_{n,3}$. In this paper, we present a sharp upper bound for
$S_{n,3}$. In this paper, we present a sharp upper bound for 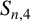 $S_{n,4}$ and characterise the sequences
$S_{n,4}$ and characterise the sequences 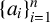 $\{a_i\}_{i=1}^n$ for which the upper bound is attained.
$\{a_i\}_{i=1}^n$ for which the upper bound is attained.
MSC classification
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 107 , Issue 1 , February 2023 , pp. 10 - 21
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
This work was supported in part by research grants from the Natural Sciences and Engineering Research Council of Canada (Grant No. DDG-2019-04206 and RGPIN 2017-03903).


