Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Browne, Patrick J.
1971.
A class of linear operators.
Bulletin of the Australian Mathematical Society,
Vol. 4,
Issue. 3,
p.
429.
Browne, Patrick J.
1975.
Commuting k-Tuples of Self Adjoint Operators and Matrix Measures.
Canadian Mathematical Bulletin,
Vol. 18,
Issue. 3,
p.
321.

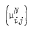 ,
, 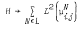 such that
such that 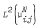 , is the multiplication operator
, is the multiplication operator 