Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jorgensen, Palle E. T.
Kornelson, Keri A.
and
Shuman, Karen L.
2011.
Families of Spectral Sets for Bernoulli Convolutions.
Journal of Fourier Analysis and Applications,
Vol. 17,
Issue. 3,
p.
431.
Dutkay, Dorin
and
Jorgensen, Palle
2012.
Spectral measures and Cuntz algebras.
Mathematics of Computation,
Vol. 81,
Issue. 280,
p.
2275.
Dutkay, Dorin
and
Jorgensen, Palle
2012.
Fourier duality for fractal measures with affine scales.
Mathematics of Computation,
Vol. 81,
Issue. 280,
p.
2253.
Abbas, Mujahid
Anjum, Rizwan
and
Iqbal, Hira
2022.
Generalized enriched cyclic contractions with application to generalized iterated function system.
Chaos, Solitons & Fractals,
Vol. 154,
Issue. ,
p.
111591.

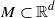 . An invariant set is defined to be a nonempty set
. An invariant set is defined to be a nonempty set 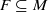 satisfying
satisfying 