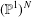Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ghioca, Dragos
and
Saleh, Sina
2022.
Zariski dense orbits for regular self-maps on split semiabelian varieties.
Canadian Mathematical Bulletin,
Vol. 65,
Issue. 1,
p.
116.
Mello, Jorge
2022.
On semigroup orbits of polynomials in multiplicative subgroups.
Monatshefte für Mathematik,
Vol. 197,
Issue. 1,
p.
177.
Mavraki, Niki Myrto
Schmidt, Harry
and
Wilms, Robert
2023.
Height coincidences in products of the projective line.
Mathematische Zeitschrift,
Vol. 304,
Issue. 2,
Schmidt, Harry
2023.
Polynomial dynamics and local analysis of small and grand orbits.
Compositio Mathematica,
Vol. 159,
Issue. 1,
p.
53.
Bell, Jason
Ghioca, Dragos
and
Reichstein, Zinovy
2024.
Rational self-maps with a regular iterate on a semiabelian variety.
Journal of Number Theory,
Vol. 260,
Issue. ,
p.
103.
Mavraki, Niki Myrto
and
Schmidt, Harry
2025.
On the dynamical Bogomolov conjecture for families of split rational maps.
Duke Mathematical Journal,
Vol. 174,
Issue. 5,