No CrossRef data available.
Published online by Cambridge University Press: 17 February 2016
We revisit Berkovich and Garvan’s two bijections: the first gives symmetry of cranks and the second relates partitions with crank 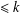 $\leq k$ to those with
$\leq k$ to those with 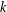 $k$ in the rank-set of partitions. Using these, we give a combinatorial proof for the relationship between the first positive crank moment and the sum of sizes of Durfee squares. We also study refinements of the first and second positive crank moments.
$k$ in the rank-set of partitions. Using these, we give a combinatorial proof for the relationship between the first positive crank moment and the sum of sizes of Durfee squares. We also study refinements of the first and second positive crank moments.