Article contents
RADICAL RELATED TO SPECIAL ATOMS REVISITED
Published online by Cambridge University Press: 14 October 2014
Abstract
A semiprime ring 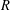 $R$ is called a
$R$ is called a  $\ast$-ring if the factor ring
$\ast$-ring if the factor ring 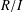 $R/I$ is in the prime radical for every nonzero ideal
$R/I$ is in the prime radical for every nonzero ideal 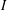 $I$ of
$I$ of 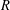 $R$. A long-standing open question posed by Gardner asks whether the prime radical coincides with the upper radical
$R$. A long-standing open question posed by Gardner asks whether the prime radical coincides with the upper radical 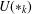 $U(\ast _{k})$ generated by the essential cover of the class of all
$U(\ast _{k})$ generated by the essential cover of the class of all  $\ast$-rings. This question is related to many other open questions in radical theory which makes studying properties of
$\ast$-rings. This question is related to many other open questions in radical theory which makes studying properties of 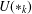 $U(\ast _{k})$ worthwhile. We show that
$U(\ast _{k})$ worthwhile. We show that 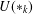 $U(\ast _{k})$ is an N-radical and that it coincides with the prime radical if and only if it is complemented in the lattice
$U(\ast _{k})$ is an N-radical and that it coincides with the prime radical if and only if it is complemented in the lattice 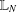 $\mathbb{L}_{N}$ of all N-radicals. Along the way, we show how to establish left hereditariness and left strongness of important upper radicals and give a complete description of all the complemented elements in
$\mathbb{L}_{N}$ of all N-radicals. Along the way, we show how to establish left hereditariness and left strongness of important upper radicals and give a complete description of all the complemented elements in 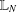 $\mathbb{L}_{N}$.
$\mathbb{L}_{N}$.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © 2014 Australian Mathematical Publishing Association Inc.
References
- 1
- Cited by

