Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-01-11T17:38:17.326Z Has data issue: false hasContentIssue false
  • English
  • Français

QUASICONTINUITY, NONATTRACTING POINTS, DISTRIBUTIVE CHAOS AND RESISTANCE TO DISRUPTIONS

Part of: Topological dynamics Maps and general types of spaces defined by maps Real functions

Published online by Cambridge University Press:  06 October 2022

MELANIA KUCHARSKA Open the ORCID record for MELANIA KUCHARSKA [Opens in a new window]  and
RYSZARD J. PAWLAK Open the ORCID record for RYSZARD J. PAWLAK [Opens in a new window]
MELANIA KUCHARSKA
Affiliation:
Faculty of Mathematics and Computer Science, University of Lodz, Banacha 22, 90-238 Lodz, Poland e-mail: melania.kucharska@edu.uni.lodz.pl
RYSZARD J. PAWLAK*
Affiliation:
Faculty of Mathematics and Computer Science, University of Lodz, Banacha 22, 90-238 Lodz, Poland
*
e-mail: ryszard.pawlak@wmii.uni.lodz.pl
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that any continuous function can be locally approximated at a fixed point 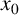$x_{0}$ by an uncountable family resistant to disruptions by the family of continuous functions for which $x_{0}$ is a fixed point. In that context, we also consider the property of quasicontinuity.

Keywords

quasicontinuitydistributive chaosDC1 pointnonattracting pointresistance to disruptions

MSC classification

Primary: 26A18: Iteration
Secondary: 37B40: Topological entropy 26A15: Continuity and related questions (modulus of continuity, semicontinuity, discontinuities, etc.) 54C70: Entropy
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 107 , Issue 1 , February 2023 , pp. 102 - 111
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cao, J. and McCluskey, A., ‘Topological transitivity in quasi-continuous dynamical systems’, Topology Appl. 301 (2021), Article no. 107496.CrossRefGoogle Scholar
Čiklová, M., ‘Dynamical systems generated by functions with connected ${G}_{\delta }$ graphs’, Real Anal. Exchange 30(2) (2005), 617–638.CrossRefGoogle Scholar
Crannel, A. and Martelli, M., ‘Dynamics of quasicontinuous systems’, J. Difference Equ. Appl. 6(3) (2000), 351–361.CrossRefGoogle Scholar
Devaney, R. L., An Introduction to Chaotic Dynamical Systems, 2nd edn (Addison-Wesley Publishing Company, Redwood City, CA, 1989).Google Scholar
Kempisty, S., ‘Sur les fonctions quasicontinues’, Fund. Math. 19(1) (1932), 184–197.CrossRefGoogle Scholar
Korczak-Kubiak, E., Loranty, A. and Pawlak, R. J., ‘On points focusing entropy’, Entropy 20(2) (2018), Article no. 128.CrossRefGoogle ScholarPubMed
Loranty, A. and Pawlak, R. J., ‘On the local aspects of distributional chaos’, Chaos 29(1) (2019), Article no. 013104.Google Scholar
Pawlak, H. and Pawlak, R. J., ‘The stable points and the attractors of Darboux functions’, Tatra Mt. Math. Publ. 40 (2008), 13–24.Google Scholar
Pawlak, H. and Pawlak, R. J., ‘Dynamics of Darboux functions’, Tatra Mt. Math. Publ. 42 (2009), 51–60.Google Scholar
Pawlak, R. J., ‘Distortion of dynamical systems in the context of focusing the chaos around the point’, Internat. J. Bifur. Chaos Appl. Sci. Engrg. 28(1) (2018), Article no. 1850006, 13 pages.CrossRefGoogle Scholar
Poprawa, J., Lokalne Aspekty Entropii i Chaosu Dyskretnych Układów Dynamicznych, Doctoral Thesis, Łódź, 2021.Google Scholar
Ruette, S., Chaos on the Interval—A Survey of Relationship Between the Various Kinds of Chaos for Continuous Interval Maps, University Lecture Series, 67 (American Mathematical Society, Providence, RI, 2017).Google Scholar
Schweizer, B. and Smítal, J., ‘Measures of chaos and a spectral decomposition of dynamical systems on the interval’, Trans. Amer. Math. Soc. 344(2) (1994), 737–754.CrossRefGoogle Scholar