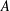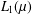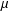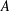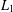Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tu, Kun
2021.
Quantitative weakly compact sets and Banach-Saks sets in $$\ell _1$$.
Archiv der Mathematik,
Vol. 117,
Issue. 3,
p.
315.