No CrossRef data available.
Article contents
PROPERTY L AND COMMUTING EXPONENTIALS IN DIMENSION AT MOST THREE
Part of:
Basic linear algebra
Published online by Cambridge University Press: 28 June 2013
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let 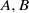 $A, B$ be two square complex matrices of the same dimension
$A, B$ be two square complex matrices of the same dimension 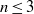 $n\leq 3$. We show that the following conditions are equivalent. (i) There exists a finite subset
$n\leq 3$. We show that the following conditions are equivalent. (i) There exists a finite subset 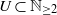 $U\subset { \mathbb{N} }_{\geq 2} $ such that for every
$U\subset { \mathbb{N} }_{\geq 2} $ such that for every 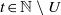 $t\in \mathbb{N} \setminus U$,
$t\in \mathbb{N} \setminus U$, 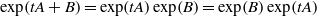 $\exp (tA+ B)= \exp (tA)\exp (B)= \exp (B)\exp (tA)$. (ii) The pair
$\exp (tA+ B)= \exp (tA)\exp (B)= \exp (B)\exp (tA)$. (ii) The pair  $(A, B)$ has property L of Motzkin and Taussky and
$(A, B)$ has property L of Motzkin and Taussky and  $\exp (A+ B)= \exp (A)\exp (B)= \exp (B)\exp (A)$. We also characterise the pairs of real matrices
$\exp (A+ B)= \exp (A)\exp (B)= \exp (B)\exp (A)$. We also characterise the pairs of real matrices 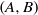 $(A, B)$ of dimension three, that satisfy the previous conditions.
$(A, B)$ of dimension three, that satisfy the previous conditions.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright ©2013 Australian Mathematical Publishing Association Inc.
References
Baribeau, L. and Roy, S., ‘Caractérisation spectrale de la forme de Jordan’, Linear Algebra Appl. 320 (2000), 183–191.Google Scholar
Bourgeois, G., ‘On commuting exponentials in low dimensions’, Linear Algebra Appl. 423 (2007), 277–286.Google Scholar
Higham, N. J., Functions of Matrices: Theory and Computation (SIAM, Philadelphia, PA, 2008).CrossRefGoogle Scholar
Hille, E., ‘On roots and logarithms of elements of a complex Banach algebra’, Math. Ann. 136 (1958), 46–57.Google Scholar
Horn, R. and Piepmeyer, G., ‘Two applications of the theory of primary matrix functions’, Linear Algebra Appl. 361 (2003), 99–106.CrossRefGoogle Scholar
Morinaga, K. and Nôno, T., ‘On the non-commutative solutions of the exponential equation  ${e}^{x} {e}^{y} = {e}^{x+ y} $’, J. Sci. Hiroshima Univ. Ser. A 17 (1954), 345–358.Google Scholar
${e}^{x} {e}^{y} = {e}^{x+ y} $’, J. Sci. Hiroshima Univ. Ser. A 17 (1954), 345–358.Google Scholar
Morinaga, K. and Nôno, T., ‘On the non-commutative solutions of the exponential equation  ${e}^{x} {e}^{y} = {e}^{x+ y} $, II’, J. Sci. Hiroshima Univ. Ser. A 18 (1954), 137–178.Google Scholar
${e}^{x} {e}^{y} = {e}^{x+ y} $, II’, J. Sci. Hiroshima Univ. Ser. A 18 (1954), 137–178.Google Scholar
Motzkin, T. S. and Taussky, O., ‘Pairs of matrices with property L’, Trans. Amer. Math. Soc. 73 (1952), 108–114.Google Scholar
Schmoeger, Ch., ‘Remarks on commuting exponentials in Banach algebras. II’, Proc. Amer. Math. Soc. 128 (11) (2000), 3405–3409.CrossRefGoogle Scholar
de Seguins Pazzis, C., ‘On commuting matrices and exponentials’, Proc. Amer. Math. Soc. 141 (2013), 763–774.Google Scholar
Wermuth, E. M. E., ‘Two remarks on matrix exponentials’, Linear Algebra Appl. 117 (1989), 127–132.Google Scholar

