No CrossRef data available.
Article contents
PRODUCT FRACTAL SETS DETERMINED BY STABLE PROCESSES
Published online by Cambridge University Press: 26 February 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let Xi be transient βi-stable processes on ℝdi, i=1,2. Assume further that X1 and X2 are independent. We shall find the exact Hausdorff measure function for the product sets R1(1)×R2(1), where 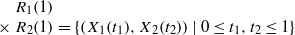 . The result of Hu generalizes [Some fractal sets determined by stable processes, Probab. Theory Related Fields 100 (1994), 205–225].
. The result of Hu generalizes [Some fractal sets determined by stable processes, Probab. Theory Related Fields 100 (1994), 205–225].
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 2009
Footnotes
Research supported by NSFC Grant 10601047 and 2008XNM06.
References
[1] Falconer, K. J., Fractal Geometry: Mathematical Foundations and Applications (Wiley, Chichester, 1990).Google Scholar
[2] Hu, X. Y., ‘Some fractal sets determined by stable processes’, Probab. Theory Related Fields 100 (1994), 205–225.CrossRefGoogle Scholar
[3] Pruitt, W. E. and Taylor, S. J., ‘Sample path properties of processes with stable components’, Z. Wahrsch. Verw. Gebiete 12 (1969), 267–289.CrossRefGoogle Scholar
[4] Rogers, C. A. and Taylor, S. J., ‘Functions continuous and singular with respect to a Hausdorff measure’, Mathematika 8 (1961), 1–31.CrossRefGoogle Scholar
[5] Taylor, S. J., ‘Sample path properties of a transient stable process’, J. Math. Mech. 16 (1967), 1229–1246.Google Scholar

