No CrossRef data available.
Article contents
Permutational labelling of constant weight Gray codes
Published online by Cambridge University Press: 17 April 2009
Abstract
We prove that for positive integers n and r satisfying 1 < r < n, with the single exception of n = 4 and r = 2, there exists a constant weight Gray code of r-sets of Xn = {1, 2, …, n} that admits an orthogonal labelling by distinct partitions, with each subsequent partition obtained from the previous one by an application of a permutation of the underlying set. Specifically, an r-set A and a partition π of Xn are said to be orthogonal if every class of π meets A in exactly one element. We prove that for all n and r as stated, and 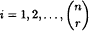 taken modulo
taken modulo 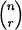 , there exists a list
, there exists a list  of the distinct r-sets of Xn with |Ai ∩ Ai+1| = r − 1 and a list of distinct partitions
of the distinct r-sets of Xn with |Ai ∩ Ai+1| = r − 1 and a list of distinct partitions 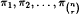 such that πi is orthogonal to both Ai and Ai+1, and πi+1 = πiλi for a suitable permutation λi of Xn.
such that πi is orthogonal to both Ai and Ai+1, and πi+1 = πiλi for a suitable permutation λi of Xn.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 2002

