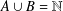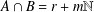Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
CHEN, SHI-QIANG
TANG, MIN
and
YANG, QUAN-HUI
2019.
ON A PROBLEM OF CHEN AND LEV.
Bulletin of the Australian Mathematical Society,
Vol. 99,
Issue. 1,
p.
15.
YAN, XIAO-HUI
2019.
ON PARTITIONS OF NONNEGATIVE INTEGERS AND REPRESENTATION FUNCTIONS.
Bulletin of the Australian Mathematical Society,
Vol. 99,
Issue. 03,
p.
385.
Chen, Shi-Qiang
and
Yan, Xiao-Hui
2020.
On certain properties of partitions of Zm with the same representation function.
Discrete Mathematics,
Vol. 343,
Issue. 9,
p.
111981.
Chen, Shi-Qiang
and
Chen, Yong-Gao
2021.
Integer sets with identical representation functions, II.
European Journal of Combinatorics,
Vol. 94,
Issue. ,
p.
103293.
Sun, C.-F.
Xiong, M.-C.
and
Yang, Q.-H.
2021.
Constructing finite sets from their representation functions.
Acta Mathematica Hungarica,
Vol. 165,
Issue. 1,
p.
134.
CHEN, SHI-QIANG
and
YAN, XIAO-HUI
2021.
PARTITIONS OF WITH IDENTICAL REPRESENTATION FUNCTION.
Bulletin of the Australian Mathematical Society,
Vol. 103,
Issue. 2,
p.
204.
Chen, Shi-Qiang
2022.
On certain properties of partitions of $$\mathbb {Z}_m$$ with the same representation function, II.
Periodica Mathematica Hungarica,
Vol. 85,
Issue. 1,
p.
177.
Sun, Cui-Fang
and
Cheng, Zhi
2022.
On the structure of finite sets with the same representation functions.
Journal of Number Theory,
Vol. 241,
Issue. ,
p.
352.
Sun, Cui-Fang
and
Xiong, Meng-Chi
2022.
On a problem of partitions of $$\mathbb {Z}_{m}$$ with the same representation functions.
Periodica Mathematica Hungarica,
Vol. 85,
Issue. 1,
p.
140.
JIAO, KAI-JIE
SÁNDOR, CSABA
YANG, QUAN-HUI
and
ZHOU, JUN-YU
2022.
ON INTEGER SETS WITH THE SAME REPRESENTATION FUNCTIONS.
Bulletin of the Australian Mathematical Society,
Vol. 106,
Issue. 2,
p.
224.
Sun, Cui-Fang
and
Pan, Hao
2023.
Partitions of Finite Nonnegative Integer Sets with Identical Representation Functions.
Bulletin of the Iranian Mathematical Society,
Vol. 49,
Issue. 3,
Sun, Cui-Fang
2024.
On finite nonnegative integer sets with identical representation functions.
The Ramanujan Journal,
Vol. 65,
Issue. 1,
p.
429.
Sun, Cuifang
2024.
On the Structure of Finite Sets with Identical Representation Functions.
Frontiers of Mathematics,
Vol. 19,
Issue. 4,
p.
665.
Sun, Cui-Fang
and
Pan, Hao
2025.
On the structure of non-negative integer sets which have identical representation functions.
Proceedings of the Edinburgh Mathematical Society,
Vol. 68,
Issue. 2,
p.
655.
Sun, Cui-Fang
and
Cheng, Zhi
2025.
Partitions of Zm with identical representation functions.
Discrete Applied Mathematics,
Vol. 362,
Issue. ,
p.
1.
Sun, Cuifang
2025.
Representation Functions on the Additive Group of Residue Classes.
Chinese Annals of Mathematics, Series B,
Vol. 46,
Issue. 2,
p.
233.