No CrossRef data available.
Article contents
ON THE PROBABILITY DISTRIBUTION OF THE PRODUCT OF POWERS OF ELEMENTS IN COMPACT LIE GROUPS
Published online by Cambridge University Press: 17 May 2019
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In this paper, we study the probability distribution of the word map 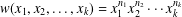 $w(x_{1},x_{2},\ldots ,x_{k})=x_{1}^{n_{1}}x_{2}^{n_{2}}\cdots x_{k}^{n_{k}}$ in a compact Lie group. We show that the probability distribution can be represented as an infinite series. Moreover, in the case of the Lie group
$w(x_{1},x_{2},\ldots ,x_{k})=x_{1}^{n_{1}}x_{2}^{n_{2}}\cdots x_{k}^{n_{k}}$ in a compact Lie group. We show that the probability distribution can be represented as an infinite series. Moreover, in the case of the Lie group  $\text{SU}(2)$, our computations give a nice convergent series for the probability distribution.
$\text{SU}(2)$, our computations give a nice convergent series for the probability distribution.
MSC classification
Secondary:
43A80: Analysis on other specific Lie groups
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 100 , Issue 3 , December 2019 , pp. 440 - 445
- Copyright
- © 2019 Australian Mathematical Publishing Association Inc.
Footnotes
This research is funded by the Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 101.04-2015.20.
References
Bröcker, T. and Dieck, T. T., Representations of Compact Lie Groups, Graduate Texts in Mathematics, 98 (Springer, Berlin–Heidelberg, 2013).Google Scholar
Das, A. K. and Nath, R. K., ‘On solutions of a class of equations in a finite group’, Comm. Algebra
37(11) (2009), 3904–3911.10.1080/00927870902828777Google Scholar
Erdős, P. and Turán, P., ‘On some problems of statistical group theory I’, Z. Wahrscheinlichkeitstheorie verw. Geb.
4 (1965), 175–186.10.1007/BF00536750Google Scholar
Erdős, P. and Turán, P., ‘On some problems of statistical group theory IV’, Acta Math. Acad. Sci. Hungar.
19 (1968), 413–435.10.1007/BF01894517Google Scholar
Erfanian, A. and Rezaei, R., ‘On the commutativity degree of compact groups’, Arch. Math. (Basel)
93 (2009), 201–212.Google Scholar
Garion, S. and Shalev, A., ‘Commutator maps, measure preservation, and T-systems’, Trans. Amer. Math. Soc.
361(9) (2009), 4631–4651.10.1090/S0002-9947-09-04575-9Google Scholar
Hofmann, K. H. and Russo, F. G., ‘The probability that x and y commute in a compact group’, Math. Proc. Cambridge Philos. Soc.
153(3) (2012), 557–571.10.1017/S0305004112000308Google Scholar
Hofmann, K. H. and Russo, F. G., ‘The probability that x
m
and y
n
commute in a compact group’, Bull. Aust. Math. Soc.
87(3) (2013), 503–513.10.1017/S0004972712000573Google Scholar
Jeffrey, A. and Zwillinger, D. (eds.), Tables of Integrals, Series, and Products, 7th edn (Elsevier, Burlington, MA, 2007).Google Scholar
Larsen, M. and Shalev, A., ‘On the distribution of values of certain word maps’, Trans. Amer. Math. Soc.
368(3) (2016), 1647–1661.10.1090/tran/6389Google Scholar
Mason, J. C. and Handscomb, D. C., Chebyshev Polynomials (Chapman and Hall/CRC, Boca Raton, FL, 2003).Google Scholar
Mulase, M. and Penkava, M., ‘Volume of representation varieties’, Preprint, 2002, arXiv:math/0212012.Google Scholar
Nath, R. K. and Prajapati, S. K., ‘On the number of solutions of a generalized commutator equation in finite groups’, Acta Math. Hungar.
156(1) (2018), 18–37.10.1007/s10474-018-0863-2Google Scholar
Parzanchevski, O. and Schul, G., ‘On the Fourier expansion of word maps’, Bull. Lond. Math. Soc.
46(1) (2014), 91–102.10.1112/blms/bdt068Google Scholar
Pournaki, M. R. and Sobhani, R., ‘Probability that the commutator of two group elements is equal to a given element’, J. Pure Appl. Algebra
212 (2008), 727–734.10.1016/j.jpaa.2007.06.013Google Scholar

