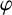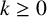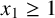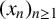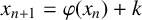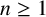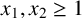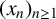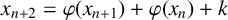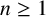1 Introduction and main results
Let
![]() $\mathbb {N}$
be the set of positive integers and fix an arithmetic function
$\mathbb {N}$
be the set of positive integers and fix an arithmetic function
![]() $f: \mathbb {N}^d\to \mathbb {N}$
for some
$f: \mathbb {N}^d\to \mathbb {N}$
for some
![]() $d \in \mathbb {N}$
. Let
$d \in \mathbb {N}$
. Let
![]() $(x_n)_{n\ge 1}$
be a sequence of positive integers which satisfies the recurrence
$(x_n)_{n\ge 1}$
be a sequence of positive integers which satisfies the recurrence
with starting values
![]() $x_1,\ldots ,x_d\in \mathbb {N}$
. In the case where
$x_1,\ldots ,x_d\in \mathbb {N}$
. In the case where
![]() $d=1$
, the sequence
$d=1$
, the sequence
![]() $(x_n)_{n\ge 1}$
is simply the orbit of
$(x_n)_{n\ge 1}$
is simply the orbit of
![]() $x_1$
with respect to f. The aim of this note is to study whether certain recurrence sequences
$x_1$
with respect to f. The aim of this note is to study whether certain recurrence sequences
![]() $(x_n)_{n\ge 1}$
of the type (1.1) are eventually periodic independent of their starting values, that is, for all
$(x_n)_{n\ge 1}$
of the type (1.1) are eventually periodic independent of their starting values, that is, for all
![]() $x_1,\ldots ,x_d \in \mathbb {N}$
, there exists
$x_1,\ldots ,x_d \in \mathbb {N}$
, there exists
![]() $T \in \mathbb {N}$
such that
$T \in \mathbb {N}$
such that
![]() $x_n=x_{n+T}$
for all sufficiently large n.
$x_n=x_{n+T}$
for all sufficiently large n.
We will frequently use the basic observation that a recurrence sequence
![]() $(x_n)_{n\ge 1}$
, as in (1.1), is eventually periodic if and only if it is bounded (see [Reference Everest, van der Poorten, Shparlinski and Ward5, page 45]).
$(x_n)_{n\ge 1}$
, as in (1.1), is eventually periodic if and only if it is bounded (see [Reference Everest, van der Poorten, Shparlinski and Ward5, page 45]).
We start with a simple result for functions f which are not too large.
Proposition 1.1. Let
![]() $f: \mathbb {N}^d \to \mathbb {N}$
be an arithmetical function, with
$f: \mathbb {N}^d \to \mathbb {N}$
be an arithmetical function, with
![]() $d \in \mathbb {N}$
, and suppose that there exists
$d \in \mathbb {N}$
, and suppose that there exists
![]() $C \in \mathbb {N}$
such that
$C \in \mathbb {N}$
such that
for all
![]() $n_1,\ldots ,n_d \in \mathbb {N}$
with
$n_1,\ldots ,n_d \in \mathbb {N}$
with
![]() $n_i \ge C$
for some
$n_i \ge C$
for some
![]() $i\in \{1,\ldots ,d\}$
. Let
$i\in \{1,\ldots ,d\}$
. Let
![]() $(x_n)_{n\ge 1}$
be a recurrence sequence as in (1.1), with starting values
$(x_n)_{n\ge 1}$
be a recurrence sequence as in (1.1), with starting values
![]() $x_1,\ldots ,x_d \in \mathbb {N}$
. Then
$x_1,\ldots ,x_d \in \mathbb {N}$
. Then
In particular,
![]() $(x_n)_{n\ge 1}$
is bounded above and hence eventually periodic.
$(x_n)_{n\ge 1}$
is bounded above and hence eventually periodic.
Special instances of Proposition 1.1 in the one-dimensional case
![]() $d=1$
have been previously obtained in the literature. For example, Porges [Reference Porges15] considered the case where
$d=1$
have been previously obtained in the literature. For example, Porges [Reference Porges15] considered the case where
![]() $f(n)$
is the sum of squares of the digits of n (see also [Reference Isaacs7, Reference Lorenzini, Melistas, Suresh, Suwama and Wang11, Reference Stewart19]). Note that (1.2) holds if
$f(n)$
is the sum of squares of the digits of n (see also [Reference Isaacs7, Reference Lorenzini, Melistas, Suresh, Suwama and Wang11, Reference Stewart19]). Note that (1.2) holds if
![]() $f(n_1,\ldots ,n_d)=o(N)$
as
$f(n_1,\ldots ,n_d)=o(N)$
as
![]() $N=\max \{n_1,\ldots ,n_d\}\to \infty $
.
$N=\max \{n_1,\ldots ,n_d\}\to \infty $
.
Of course, there exist other functions f which do not satisfy (1.2) and such that every sequence
![]() $(x_n)_{n\ge 1}$
, as in (1.1), is eventually periodic: as a trivial example, one can consider
$(x_n)_{n\ge 1}$
, as in (1.1), is eventually periodic: as a trivial example, one can consider
![]() $f(n_1,\ldots ,n_d):=\max \{n_1,\ldots ,n_d\}$
for all
$f(n_1,\ldots ,n_d):=\max \{n_1,\ldots ,n_d\}$
for all
![]() $(n_1,\ldots ,n_d) \in \mathbb {N}^d$
. At the opposite extreme, if f is slightly bigger (for instance,
$(n_1,\ldots ,n_d) \in \mathbb {N}^d$
. At the opposite extreme, if f is slightly bigger (for instance,
![]() $f(n_1,\ldots ,n_d):=\max \{n_1,\ldots ,n_d\}+1$
), then there are no eventually periodic sequences
$f(n_1,\ldots ,n_d):=\max \{n_1,\ldots ,n_d\}+1$
), then there are no eventually periodic sequences
![]() $(x_n)_{n\ge 1}$
as in (1.1). This is the starting point for this work, which motivates the heuristic: if a function f satisfies (1.2) ‘on average’, then every sequence
$(x_n)_{n\ge 1}$
as in (1.1). This is the starting point for this work, which motivates the heuristic: if a function f satisfies (1.2) ‘on average’, then every sequence
![]() $(x_{n})_{n\ge 1}$
as in (1.1) should be eventually periodic, independent of its starting values.
$(x_{n})_{n\ge 1}$
as in (1.1) should be eventually periodic, independent of its starting values.
We are going to confirm the above heuristic in two cases which involve (shifted iterates of) Euler’s function
![]() $\varphi $
(recall that
$\varphi $
(recall that
![]() $\varphi (n)$
is the number of integers in
$\varphi (n)$
is the number of integers in
![]() $\{1,\ldots ,n\}$
which are coprime with n). Our first main result is the following theorem.
$\{1,\ldots ,n\}$
which are coprime with n). Our first main result is the following theorem.
Theorem 1.2. Fix an integer
![]() $k\ge 0$
and let
$k\ge 0$
and let
![]() $(x_n)_{n\ge 1}$
be the recurrence sequence defined by
$(x_n)_{n\ge 1}$
be the recurrence sequence defined by
with starting value
![]() $x_1 \in \mathbb {N}$
. Then,
$x_1 \in \mathbb {N}$
. Then,
In particular,
![]() $(x_n)_{n\ge 1}$
is eventually periodic.
$(x_n)_{n\ge 1}$
is eventually periodic.
Note that the dependence of the upper bound (1.4) on
![]() $x_1$
cannot be removed: indeed, if
$x_1$
cannot be removed: indeed, if
![]() $k:=x_1-\varphi (x_1)$
for some
$k:=x_1-\varphi (x_1)$
for some
![]() $x_1\in \mathbb {N}$
, then the sequence
$x_1\in \mathbb {N}$
, then the sequence
![]() $(x_{n})_{n\ge 1}$
is constantly equal to
$(x_{n})_{n\ge 1}$
is constantly equal to
![]() $x_1$
.
$x_1$
.
The trivial case
![]() $k=0$
in Theorem 1.2 has been already considered in the literature from different viewpoints (and, of course, it follows by Proposition 1.1 since
$k=0$
in Theorem 1.2 has been already considered in the literature from different viewpoints (and, of course, it follows by Proposition 1.1 since
![]() $\varphi (n)\le n-1$
for all
$\varphi (n)\le n-1$
for all
![]() $n\ge 2$
). Indeed, given a starting value
$n\ge 2$
). Indeed, given a starting value
![]() $x_1 \in \mathbb {N}$
, then
$x_1 \in \mathbb {N}$
, then
![]() $x_{n+1}=\varphi ^{(n)}(x_1)$
for all
$x_{n+1}=\varphi ^{(n)}(x_1)$
for all
![]() $n \in \mathbb {N}$
, where
$n \in \mathbb {N}$
, where
![]() $\varphi ^{(m)}$
is the m-fold iteration of
$\varphi ^{(m)}$
is the m-fold iteration of
![]() $\varphi $
. For instance, Pillai [Reference Pillai12] showed that
$\varphi $
. For instance, Pillai [Reference Pillai12] showed that
 $$ \begin{align*} \bigg\lfloor \frac{\log x_1-\log 2}{\log 3}\bigg\rfloor+1 \le N(x_1) \le \bigg\lfloor \frac{\log x_1}{\log 2}\bigg\rfloor+1 \quad \text{for all }x_1 \in \mathbb{N}, \end{align*} $$
$$ \begin{align*} \bigg\lfloor \frac{\log x_1-\log 2}{\log 3}\bigg\rfloor+1 \le N(x_1) \le \bigg\lfloor \frac{\log x_1}{\log 2}\bigg\rfloor+1 \quad \text{for all }x_1 \in \mathbb{N}, \end{align*} $$
where
![]() $N(x_1)$
is the minimal integer n for which
$N(x_1)$
is the minimal integer n for which
![]() $x_n=1$
(see also [Reference Shapiro17]) and it has been conjectured by Erdős et al. [Reference Erdős, Granville, Pomerance, Spiro, Berndt, Diamond, Halberstam and Hildebrand4] that
$x_n=1$
(see also [Reference Shapiro17]) and it has been conjectured by Erdős et al. [Reference Erdős, Granville, Pomerance, Spiro, Berndt, Diamond, Halberstam and Hildebrand4] that
![]() $N(x_1) \sim \alpha \log x_1$
as
$N(x_1) \sim \alpha \log x_1$
as
![]() $x_1\to \infty $
, for some
$x_1\to \infty $
, for some
![]() $\alpha \in \mathbb {R}$
. It is known that the understanding of the multiplicative structure of
$\alpha \in \mathbb {R}$
. It is known that the understanding of the multiplicative structure of
![]() $\varphi $
and its iterates is, in some sense, equivalent to the study of the behaviour of the integers of the form
$\varphi $
and its iterates is, in some sense, equivalent to the study of the behaviour of the integers of the form
![]() $p-1$
, where p is a prime. See also [Reference Lamzouri8, Reference Loomis and Luca10, Reference Pollack14, Reference Shparlinski18] for related work.
$p-1$
, where p is a prime. See also [Reference Lamzouri8, Reference Loomis and Luca10, Reference Pollack14, Reference Shparlinski18] for related work.
However, if
![]() $k\ge 1$
, then the function
$k\ge 1$
, then the function
![]() $f(n):=\varphi (n)+k$
does not satisfy (1.2): indeed,
$f(n):=\varphi (n)+k$
does not satisfy (1.2): indeed,
![]() $\varphi (p)=p-1$
for all primes p, and hence
$\varphi (p)=p-1$
for all primes p, and hence
![]() $f(p)\ge p$
. However, it is well known that
$f(p)\ge p$
. However, it is well known that
 $$ \begin{align} \frac{1}{n}\sum_{i=1}^n \varphi(i)=\frac{3}{\pi^2}n+O(\log n) \quad \text{as }n\to \infty \end{align} $$
$$ \begin{align} \frac{1}{n}\sum_{i=1}^n \varphi(i)=\frac{3}{\pi^2}n+O(\log n) \quad \text{as }n\to \infty \end{align} $$
(see, for example, [Reference De Koninck and Luca2, Theorem 8.6]). Hence, approximating roughly
![]() $f(n)$
with
$f(n)$
with
![]() $cn+k$
, where
$cn+k$
, where
![]() $c=3/\pi ^2 \in (0,1)$
, we expect that (1.2) holds ‘on average’, which is the heuristic behind Theorem 1.2.
$c=3/\pi ^2 \in (0,1)$
, we expect that (1.2) holds ‘on average’, which is the heuristic behind Theorem 1.2.
Our second main result is the following theorem.
Theorem 1.3. Fix an even integer
![]() $k\ge 0$
and let
$k\ge 0$
and let
![]() $(x_n)_{n\ge 1}$
be the recurrence sequence defined by
$(x_n)_{n\ge 1}$
be the recurrence sequence defined by
with starting values
![]() $x_1,x_2 \in \mathbb {N}$
. Then,
$x_1,x_2 \in \mathbb {N}$
. Then,
In particular,
![]() $(x_n)_{n\ge 1}$
is eventually periodic.
$(x_n)_{n\ge 1}$
is eventually periodic.
The heuristic supporting Theorem 1.3 is similar: thanks to (1.5), the value
![]() $f(n,m):=\varphi (n)+\varphi (m)+k$
can be roughly bounded above by
$f(n,m):=\varphi (n)+\varphi (m)+k$
can be roughly bounded above by
![]() $2c\max \{n,m\}+k$
, which is definitely smaller than
$2c\max \{n,m\}+k$
, which is definitely smaller than
![]() $\max \{n,m\}$
since
$\max \{n,m\}$
since
![]() $2c=6/\pi ^2 <1$
.
$2c=6/\pi ^2 <1$
.
We end with an open question to check if d is sufficiently large, then there exist starting values
![]() $x_1,\ldots ,x_d \in \mathbb {N}$
such that the sequence
$x_1,\ldots ,x_d \in \mathbb {N}$
such that the sequence
![]() $(x_n)_{n\ge 1}$
defined as in (1.1) with
$(x_n)_{n\ge 1}$
defined as in (1.1) with
is not eventually periodic. In a sense, this is related to the open question known as Lehmer’s totient problem [Reference Lehmer9], which asks about the existence of a composite
![]() $q\ge 2$
such that
$q\ge 2$
such that
![]() $\varphi (q)$
divides
$\varphi (q)$
divides
![]() $q-1$
: indeed, if
$q-1$
: indeed, if
![]() $r:=(q-1)/\varphi (q)$
,
$r:=(q-1)/\varphi (q)$
,
![]() $d=r$
and
$d=r$
and
![]() $x_1=\cdots =x_d=q$
, then the sequence
$x_1=\cdots =x_d=q$
, then the sequence
![]() $(x_n)_{n\ge 1}$
would be constant.
$(x_n)_{n\ge 1}$
would be constant.
Lastly, as suggested by the referee, it would be interesting to check whether the upper estimates of our main results are, in some sense, sufficiently sharp and whether some nontrivial lower bounds on the size of
![]() $(x_n)_{n\ge 1}$
could be obtained. We do not have an answer to these questions. However, we suspect that they are quite difficult. Indeed, in the setting of Theorem 1.2, one could try to obtain a cycle with period
$(x_n)_{n\ge 1}$
could be obtained. We do not have an answer to these questions. However, we suspect that they are quite difficult. Indeed, in the setting of Theorem 1.2, one could try to obtain a cycle with period
![]() $(x_1,\ldots ,x_T)$
made by all primes in arithmetic progression but the last one (so that
$(x_1,\ldots ,x_T)$
made by all primes in arithmetic progression but the last one (so that
![]() $x_1=x_{T+1}=\varphi (x_T)+k$
). A possible interpretation may amount to asking whether such examples exist with comparable sizes of T and k.
$x_1=x_{T+1}=\varphi (x_T)+k$
). A possible interpretation may amount to asking whether such examples exist with comparable sizes of T and k.
2 Proofs
Proof of Proposition 1.1.
Let
![]() $\mathcal {Q}$
be the set of d-uples
$\mathcal {Q}$
be the set of d-uples
![]() $(n_1,\ldots ,n_d) \in \mathbb {N}^d$
with
$(n_1,\ldots ,n_d) \in \mathbb {N}^d$
with
![]() $n_i\le C-1$
for all
$n_i\le C-1$
for all
![]() $i \in \{1,\ldots ,d\}$
. Suppose that
$i \in \{1,\ldots ,d\}$
. Suppose that
![]() $(n_1,\ldots ,n_d) \in \mathbb {N}\setminus \mathcal {Q}$
. Hence, we can pick the largest index
$(n_1,\ldots ,n_d) \in \mathbb {N}\setminus \mathcal {Q}$
. Hence, we can pick the largest index
![]() $i \in \{1,\ldots ,d\}$
such that
$i \in \{1,\ldots ,d\}$
such that
![]() $n_i=\max \{n_1,\ldots ,n_d\}$
. In particular,
$n_i=\max \{n_1,\ldots ,n_d\}$
. In particular,
![]() $n_i\ge C$
. We claim that there exists
$n_i\ge C$
. We claim that there exists
![]() $m \in \mathbb {N}$
such that
$m \in \mathbb {N}$
such that
![]() $(n_{m+1}, \ldots , n_{m+d}) \in \mathcal {Q}$
. In addition, if m is the least such integer, then
$(n_{m+1}, \ldots , n_{m+d}) \in \mathcal {Q}$
. In addition, if m is the least such integer, then
![]() $\max \{n_j,\ldots ,n_{j+d-1}\}$
is decreasing for
$\max \{n_j,\ldots ,n_{j+d-1}\}$
is decreasing for
![]() $j \in \{1,\ldots ,m\}$
. To this aim, suppose for the sake of contradiction that the claim does not hold. By the standing hypothesis (1.2), we get
$j \in \{1,\ldots ,m\}$
. To this aim, suppose for the sake of contradiction that the claim does not hold. By the standing hypothesis (1.2), we get
![]() $n_{d+1}=f(n_1,\ldots ,n_d)< n_{i}$
. Repeating this reasoning, we obtain
$n_{d+1}=f(n_1,\ldots ,n_d)< n_{i}$
. Repeating this reasoning, we obtain
![]() $n_{d+j}< \max \{n_j,\ldots ,n_{d+j-1}\}= n_{i}$
for all
$n_{d+j}< \max \{n_j,\ldots ,n_{d+j-1}\}= n_{i}$
for all
![]() $j\in \{1,\ldots ,i\}$
. Hence,
$j\in \{1,\ldots ,i\}$
. Hence,
![]() $\max \{n_{i+1},\ldots ,n_{i+d}\}\le n_{i}~-~1$
. Proceeding similarly, it follows that
$\max \{n_{i+1},\ldots ,n_{i+d}\}\le n_{i}~-~1$
. Proceeding similarly, it follows that
However, if
![]() $k=n_{i}+1-C$
, then
$k=n_{i}+1-C$
, then
![]() $(n_{i+(k-1)d+1},\ldots ,n_{i+kd}) \in \mathcal {Q}$
, which proves the claim.
$(n_{i+(k-1)d+1},\ldots ,n_{i+kd}) \in \mathcal {Q}$
, which proves the claim.
To complete the proof, fix starting values
![]() $x_1,\ldots ,x_d \in \mathbb {N}$
. By the above claim and the finiteness of
$x_1,\ldots ,x_d \in \mathbb {N}$
. By the above claim and the finiteness of
![]() $\mathcal {Q}$
, it follows that the sequence
$\mathcal {Q}$
, it follows that the sequence
![]() $(x_n)_{n\ge 1}$
is bounded above by the constant
$(x_n)_{n\ge 1}$
is bounded above by the constant
and that the upper limit in (1.3) holds.
Proof of Theorem 1.2.
First, let us suppose
![]() $k \le 1$
and fix a starting value
$k \le 1$
and fix a starting value
![]() $x_1 \in \mathbb {N}$
. Then,
$x_1 \in \mathbb {N}$
. Then,
for all
![]() $n \in \mathbb {N}$
, with the consequence that
$n \in \mathbb {N}$
, with the consequence that
![]() $x_n \le \max \{x_1,2\}$
for all
$x_n \le \max \{x_1,2\}$
for all
![]() $n \in \mathbb {N}$
.
$n \in \mathbb {N}$
.
Suppose hereafter that
![]() $k \ge 2$
. Note that for all
$k \ge 2$
. Note that for all
![]() $n,m \in \mathbb {N}$
,
$n,m \in \mathbb {N}$
,
 $$ \begin{align} \begin{split} x_{n+m}&\le \max\{x_{n+m-1}-1,1\}+k \\ &= \max\{x_{n+m-1}+k-1,k+1\} \le \max\{x_n+m(k-1),k+1\}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} x_{n+m}&\le \max\{x_{n+m-1}-1,1\}+k \\ &= \max\{x_{n+m-1}+k-1,k+1\} \le \max\{x_n+m(k-1),k+1\}. \end{split} \end{align} $$
Let us suppose for the sake of contradiction that
![]() $(x_n)_{n\ge 1}$
is not bounded above. Hence, there exists a minimal
$(x_n)_{n\ge 1}$
is not bounded above. Hence, there exists a minimal
![]() $r_1 \in \mathbb {N}$
such that
$r_1 \in \mathbb {N}$
such that
![]() $x_{r_1} \ge k^4$
(in particular,
$x_{r_1} \ge k^4$
(in particular,
![]() $x_{r_1}>4$
).
$x_{r_1}>4$
).
Claim 2.1.
There exists
![]() $i \in \{1,\ldots ,k\}$
such that
$i \in \{1,\ldots ,k\}$
such that
![]() $x_{r_1+i}<x_{r_1}$
.
$x_{r_1+i}<x_{r_1}$
.
Proof. Since
![]() $\varphi (n) \le n-\sqrt {n}$
whenever n is composite (by the fact that there exists a divisor of n which is at most
$\varphi (n) \le n-\sqrt {n}$
whenever n is composite (by the fact that there exists a divisor of n which is at most
![]() $\sqrt {n}$
), it follows that, if
$\sqrt {n}$
), it follows that, if
![]() $x_{{r_1}+i-1}$
is composite for some
$x_{{r_1}+i-1}$
is composite for some
![]() $i \in \{1,\ldots ,k\}$
, then
$i \in \{1,\ldots ,k\}$
, then
Considering that the map
![]() $x\mapsto x-\sqrt {x}$
is increasing on
$x\mapsto x-\sqrt {x}$
is increasing on
![]() $(4,\infty )$
and using (2.1), we obtain
$(4,\infty )$
and using (2.1), we obtain
 $$ \begin{align*} \begin{split} x_{r_1+i} &\le x_{r_1}+(i-1)(k-1)-\sqrt{x_{r_1}+(i-1)(k-1)}+k\\ &\le x_{r_1}+(k-1)^2-\sqrt{k^4}+k < x_{r_1}. \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} x_{r_1+i} &\le x_{r_1}+(i-1)(k-1)-\sqrt{x_{r_1}+(i-1)(k-1)}+k\\ &\le x_{r_1}+(k-1)^2-\sqrt{k^4}+k < x_{r_1}. \end{split} \end{align*} $$
To conclude, we show that there exists some
![]() $i \in \{1,\ldots ,k\}$
for which
$i \in \{1,\ldots ,k\}$
for which
![]() $x_{{r_1}+i-1}$
is composite. Indeed, in the opposite case, these
$x_{{r_1}+i-1}$
is composite. Indeed, in the opposite case, these
![]() $x_{{r_1}+i-1}$
terms are all primes (and greater than k), and hence
$x_{{r_1}+i-1}$
terms are all primes (and greater than k), and hence
for all
![]() $i \in \{1,\ldots ,k\}$
. This is impossible, because there would exist
$i \in \{1,\ldots ,k\}$
. This is impossible, because there would exist
![]() $i \in \{1,\ldots ,k\}$
such that k divides
$i \in \{1,\ldots ,k\}$
such that k divides
![]() $x_{{r_1}+i-1}$
.
$x_{{r_1}+i-1}$
.
At this point, (2.1) and Claim 2.1 imply that there exists a minimal
![]() $i_1 \in \{1,\ldots ,k\}$
such that
$i_1 \in \{1,\ldots ,k\}$
such that
![]() $x_{r_1+i_1}< x_{r_1}$
; and hence
$x_{r_1+i_1}< x_{r_1}$
; and hence
With the same reasoning, we can construct recursively sequences of positive integers
![]() $(r_n)$
and
$(r_n)$
and
![]() $(i_n)$
such that for all
$(i_n)$
such that for all
![]() $n \in {\mathbb {N}}$
:
$n \in {\mathbb {N}}$
:
-
(i)
 $r_{n+1}$
is the minimal integer such that
$r_{n+1}$
is the minimal integer such that
 $r_{n+1}\ge r_n+i_n$
and
$r_{n+1}\ge r_n+i_n$
and
 $x_{r_{n+1}}\ge k^4$
;
$x_{r_{n+1}}\ge k^4$
; -
(ii)
 $i_{n+1}$
is the minimal integer in
$i_{n+1}$
is the minimal integer in
 $\{1,\ldots ,k\}$
such that
$\{1,\ldots ,k\}$
such that
 $x_{r_{n+1}+i_{n+1}}<x_{r_n}$
; and hence, (2.3)
$x_{r_{n+1}+i_{n+1}}<x_{r_n}$
; and hence, (2.3) $$ \begin{align} \max\{x_{r_n+i_n},\ldots,x_{r_{n+1}+i_{n+1}-1}\} \le x_{r_{n+1}}+(i_{n+1}-1)(k-1) < x_{r_{n+1}}+k^2. \end{align} $$
$$ \begin{align} \max\{x_{r_n+i_n},\ldots,x_{r_{n+1}+i_{n+1}-1}\} \le x_{r_{n+1}}+(i_{n+1}-1)(k-1) < x_{r_{n+1}}+k^2. \end{align} $$
Lastly, note that
for all
![]() $n \in \mathbb {N}$
. Using (2.2), (2.3) and (2.4), we conclude that
$n \in \mathbb {N}$
. Using (2.2), (2.3) and (2.4), we conclude that
for all
![]() $n \in \mathbb {N}$
. This proves (1.4), concluding the proof.
$n \in \mathbb {N}$
. This proves (1.4), concluding the proof.
Remark 2.2. A sketch of a shorter proof that the sequence
![]() $(x_n)_{n\ge 1}$
in Theorem 1.2 is eventually periodic goes as follows. Set
$(x_n)_{n\ge 1}$
in Theorem 1.2 is eventually periodic goes as follows. Set
![]() $y_n:=\varphi (x_n)$
for all
$y_n:=\varphi (x_n)$
for all
![]() $n \in \mathbb {N}$
and note that
$n \in \mathbb {N}$
and note that
![]() $y_n\le C n$
with
$y_n\le C n$
with
![]() $C:=\max \{x_1,k\}$
. Hence,
$C:=\max \{x_1,k\}$
. Hence,
![]() $\{y_1,\ldots ,y_n\}$
is contained in
$\{y_1,\ldots ,y_n\}$
is contained in
![]() $V_n:=\varphi (\mathbb {N})\cap [1,Cn]$
. By a classical result of Pillai [Reference Pillai13] (see also [Reference Ford6] and references therein), we have
$V_n:=\varphi (\mathbb {N})\cap [1,Cn]$
. By a classical result of Pillai [Reference Pillai13] (see also [Reference Ford6] and references therein), we have
![]() $|V_n|=o(n)$
as
$|V_n|=o(n)$
as
![]() $n\to \infty $
, and hence there exist distinct
$n\to \infty $
, and hence there exist distinct
![]() $i,j \in \mathbb {N}$
with
$i,j \in \mathbb {N}$
with
![]() $y_i=y_j$
. This implies that
$y_i=y_j$
. This implies that
![]() $x_{i+1}=x_{j+1}$
; therefore,
$x_{i+1}=x_{j+1}$
; therefore,
![]() $(x_n)_{n\ge 1}$
is eventually periodic. However, this does not lead to an effective upper bound as in (1.4).
$(x_n)_{n\ge 1}$
is eventually periodic. However, this does not lead to an effective upper bound as in (1.4).
In the proof of Theorem 1.3, we will need also the effective version of the third Mertens’ theorem given by Rosser and Schoenfeld [Reference Rosser and Schoenfeld16] in 1962 (see also [Reference Axler1, Reference Dusart3]). As usual, hereafter, we reserve the letter p for primes.
Proposition 2.3. Let
![]() $\gamma :=\lim _n(\sum _{i\le n}1/i-\log n)=0.57721\ldots $
be the Euler– Mascheroni constant. Then the following inequality holds for all
$\gamma :=\lim _n(\sum _{i\le n}1/i-\log n)=0.57721\ldots $
be the Euler– Mascheroni constant. Then the following inequality holds for all
![]() $x\ge 2{:}$
$x\ge 2{:}$
 $$ \begin{align*} \frac{e^{-\gamma}}{\log x} \bigg(1- \frac{1}{\log^2 x} \bigg) < \prod_{p\le x} \bigg( 1 - \frac{1}{p} \bigg) < \dfrac{e^{-\gamma}}{\log x} \bigg(1+ \frac{1}{2\log^2 x} \bigg). \end{align*} $$
$$ \begin{align*} \frac{e^{-\gamma}}{\log x} \bigg(1- \frac{1}{\log^2 x} \bigg) < \prod_{p\le x} \bigg( 1 - \frac{1}{p} \bigg) < \dfrac{e^{-\gamma}}{\log x} \bigg(1+ \frac{1}{2\log^2 x} \bigg). \end{align*} $$
Proof. See [Reference Rosser and Schoenfeld16, Theorem 7 and its Corollary].
Corollary 2.4. If
![]() $x\ge 6$
, then
$x\ge 6$
, then
 $$ \begin{align*} \prod_ {x<p\le x^3} \bigg( 1 - \frac{1}{p} \bigg)<\frac{1}{2}. \end{align*} $$
$$ \begin{align*} \prod_ {x<p\le x^3} \bigg( 1 - \frac{1}{p} \bigg)<\frac{1}{2}. \end{align*} $$
Proof. Thanks to Proposition 2.3, for each
![]() $r \ge 2$
, there exists
$r \ge 2$
, there exists
![]() $c_r \in (-1,\tfrac 12)$
such that
$c_r \in (-1,\tfrac 12)$
such that
 $$ \begin{align*} \prod_ {p\le r} \bigg( 1 - \frac{1}{p} \bigg) =\frac{e^{-\gamma}}{\log x} \bigg(1+ \frac{c_r}{\log^2 x} \bigg). \end{align*} $$
$$ \begin{align*} \prod_ {p\le r} \bigg( 1 - \frac{1}{p} \bigg) =\frac{e^{-\gamma}}{\log x} \bigg(1+ \frac{c_r}{\log^2 x} \bigg). \end{align*} $$
At this point, fix
![]() $x\ge 6$
. It follows that
$x\ge 6$
. It follows that
 $$ \begin{align*} \begin{split} \prod_ {x<p\le x^3} \bigg( 1 - \frac{1}{p} \bigg) &=\frac {\prod_{p \leq x^3} ( 1 - {1}/{p} )} {\prod_{p \leq x} ( 1 - {1}/{p} )}\\ &=\frac{e^{-\gamma}/(\log x^3)}{e^{-\gamma}/\log x}\cdot \frac{(1+c_{x^3}/(\log x^3)^2)}{1+c_x/(\log x)^2}\\ & < \frac{1}{3}\cdot \frac{1+0.5/ (9\log^2 x)}{1-1/(\log^2 x)} < \frac{1}{2}. \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \prod_ {x<p\le x^3} \bigg( 1 - \frac{1}{p} \bigg) &=\frac {\prod_{p \leq x^3} ( 1 - {1}/{p} )} {\prod_{p \leq x} ( 1 - {1}/{p} )}\\ &=\frac{e^{-\gamma}/(\log x^3)}{e^{-\gamma}/\log x}\cdot \frac{(1+c_{x^3}/(\log x^3)^2)}{1+c_x/(\log x)^2}\\ & < \frac{1}{3}\cdot \frac{1+0.5/ (9\log^2 x)}{1-1/(\log^2 x)} < \frac{1}{2}. \end{split} \end{align*} $$
Indeed, the last inequality is equivalent to
 $$ \begin{align*} \frac{2}{3} \bigg(1+\frac{1}{18 \log^2 x}\bigg)< 1-\frac{1}{\log^2 x}, \end{align*} $$
$$ \begin{align*} \frac{2}{3} \bigg(1+\frac{1}{18 \log^2 x}\bigg)< 1-\frac{1}{\log^2 x}, \end{align*} $$
which holds if and only if
The conclusion follows since the value of the right-hand side above is smaller than
![]() $6$
.
$6$
.
Proof of Theorem 1.3.
If
![]() $\max \{x_1,x_2\} \le 2$
and
$\max \{x_1,x_2\} \le 2$
and
![]() $k=0$
, then
$k=0$
, then
![]() $x_n=2$
for all
$x_n=2$
for all
![]() $n\ge 3$
, so the claimed (1.6) holds since
$n\ge 3$
, so the claimed (1.6) holds since
![]() $4^{X^{3^{k+1}}}\ge 4> x_n$
for all
$4^{X^{3^{k+1}}}\ge 4> x_n$
for all
![]() $n \in \mathbb {N}$
.
$n \in \mathbb {N}$
.
Suppose now that
![]() $\max \{x_1,x_2\} \ge 3$
or
$\max \{x_1,x_2\} \ge 3$
or
![]() $k \ge 1$
, and note that
$k \ge 1$
, and note that
![]() ${X= \tfrac 12(3x_1+5x_2+7k)\ge 6}$
. Then,
${X= \tfrac 12(3x_1+5x_2+7k)\ge 6}$
. Then,
![]() $\min \{x_3,x_4\}\ge 3$
; and hence,
$\min \{x_3,x_4\}\ge 3$
; and hence,
![]() $x_n$
is even for all
$x_n$
is even for all
![]() $n\ge 5$
. In addition, since
$n\ge 5$
. In addition, since
![]() $\max \{x_1,\ldots ,x_6\}\le 2X$
and
$\max \{x_1,\ldots ,x_6\}\le 2X$
and
it follows that the claimed inequality holds for all
![]() $n\le 6$
.
$n\le 6$
.
Let
![]() $(p_n)_{n\ge 1}$
be the increasing enumeration of the primes greater than X. Since
$(p_n)_{n\ge 1}$
be the increasing enumeration of the primes greater than X. Since
![]() $\prod _{i=1}^n(1-{1}/{p_i})$
converges to zero as
$\prod _{i=1}^n(1-{1}/{p_i})$
converges to zero as
![]() $n\to \infty $
by Proposition 2.3, one can find integers
$n\to \infty $
by Proposition 2.3, one can find integers
![]() $1 =: r_0 < r_1 < \cdots < r_{k+1}$
such that
$1 =: r_0 < r_1 < \cdots < r_{k+1}$
such that
 $$ \begin{align} \prod_{i=r_j}^{r_{j+1} - 1} \bigg(1 - \frac{1}{p_i}\bigg) < \frac{1}{2} <\prod_{i=r_j}^{r_{j+1} - 2} \bigg(1 - \frac{1}{p_i}\bigg) \quad \text{for all }j \in \{0, 1, \ldots, k\}. \end{align} $$
$$ \begin{align} \prod_{i=r_j}^{r_{j+1} - 1} \bigg(1 - \frac{1}{p_i}\bigg) < \frac{1}{2} <\prod_{i=r_j}^{r_{j+1} - 2} \bigg(1 - \frac{1}{p_i}\bigg) \quad \text{for all }j \in \{0, 1, \ldots, k\}. \end{align} $$
Define also
 $$ \begin{align*} q_j:=\prod_{i=r_j}^{r_{j+1} - 1}p_i \quad \text{for all }j \in \{0, 1, \ldots, k\}. \end{align*} $$
$$ \begin{align*} q_j:=\prod_{i=r_j}^{r_{j+1} - 1}p_i \quad \text{for all }j \in \{0, 1, \ldots, k\}. \end{align*} $$
Since
![]() $\{q_0,q_1,\ldots ,q_k\}$
are pairwise coprime, the Chinese remainder theorem yields the existence of some
$\{q_0,q_1,\ldots ,q_k\}$
are pairwise coprime, the Chinese remainder theorem yields the existence of some
![]() $y \in \mathbb {N}$
such that
$y \in \mathbb {N}$
such that
![]() $y\equiv j\bmod {q_j}$
for all
$y\equiv j\bmod {q_j}$
for all
![]() $j \in \{0,1,\ldots ,k\}$
. In particular,
$j \in \{0,1,\ldots ,k\}$
. In particular,
Let us suppose for the sake of contradiction that
![]() $(x_n)_{n\ge 1}$
is not bounded. Then, there exists a minimal
$(x_n)_{n\ge 1}$
is not bounded. Then, there exists a minimal
![]() $v \in \mathbb {N}$
such that
$v \in \mathbb {N}$
such that
![]() $x_v \ge 2y$
. Since
$x_v \ge 2y$
. Since
![]() $\max \{x_1,\ldots ,x_6\} \le 2X$
, it follows by (2.9) that
$\max \{x_1,\ldots ,x_6\} \le 2X$
, it follows by (2.9) that
![]() $v\ge 7$
. In particular,
$v\ge 7$
. In particular,
![]() $x_{v-1}$
and
$x_{v-1}$
and
![]() $x_{v-2}$
are even.
$x_{v-2}$
are even.
Claim 2.5.
![]() $\max \{\varphi (x_{v-1}),\varphi (x_{v-2})\} < y-k$
.
$\max \{\varphi (x_{v-1}),\varphi (x_{v-2})\} < y-k$
.
Proof. If
![]() $x_{v-1}<2y-2k$
then, by the fact that
$x_{v-1}<2y-2k$
then, by the fact that
![]() $x_{v-1}$
is even,
$x_{v-1}$
is even,
![]() $\varphi (x_{v-1}) \le \tfrac 12x_{v-1}<y-k$
. Otherwise, recalling that v is the minimal integer such that
$\varphi (x_{v-1}) \le \tfrac 12x_{v-1}<y-k$
. Otherwise, recalling that v is the minimal integer such that
![]() $x_v \ge 2y$
, then
$x_v \ge 2y$
, then
![]() $2y-2k \le x_{v-1}<2y$
. In addition,
$2y-2k \le x_{v-1}<2y$
. In addition,
![]() $x_{v-1}$
is even, so
$x_{v-1}$
is even, so
![]() $x_{v-1}=2y-2j$
for some
$x_{v-1}=2y-2j$
for some
![]() $j \in \{1,\ldots ,k\}$
. It follows that
$j \in \{1,\ldots ,k\}$
. It follows that
 $$ \begin{align*} \varphi(x_{v-1})=x_{v-1} \, {\prod_{p\;\! \mid \;\! x_{v-1}}} \bigg(1 - \frac{1}{p}\bigg) = (y-j) {\prod_{p\;\! \mid \;\! x_{v-1}}}^{\!\!\prime} \bigg(1 - \frac{1}{p}\bigg), \end{align*} $$
$$ \begin{align*} \varphi(x_{v-1})=x_{v-1} \, {\prod_{p\;\! \mid \;\! x_{v-1}}} \bigg(1 - \frac{1}{p}\bigg) = (y-j) {\prod_{p\;\! \mid \;\! x_{v-1}}}^{\!\!\prime} \bigg(1 - \frac{1}{p}\bigg), \end{align*} $$
where the last product is extended over the odd prime divisors of
![]() $x_{v-1}$
. Since, by construction, we have
$x_{v-1}$
. Since, by construction, we have
![]() $y\equiv j\bmod {q_j}$
, we obtain by (2.8) that
$y\equiv j\bmod {q_j}$
, we obtain by (2.8) that
 $$ \begin{align*} \varphi(x_{v-1}) \le (y-j) \prod_{i=r_j}^{r_{j+1} - 1} \bigg(1 - \frac{1}{p_i}\bigg)< \frac{y-j}{2} < y-k. \end{align*} $$
$$ \begin{align*} \varphi(x_{v-1}) \le (y-j) \prod_{i=r_j}^{r_{j+1} - 1} \bigg(1 - \frac{1}{p_i}\bigg)< \frac{y-j}{2} < y-k. \end{align*} $$
Note that the last inequality holds because
![]() $y>2k$
, thanks to (2.9).
$y>2k$
, thanks to (2.9).
The same argument can be repeated for
![]() $x_{v-2}$
.
$x_{v-2}$
.
We conclude by Claim 2.5 that
which is contradiction. It follows that
![]() $x_n<2y$
for all
$x_n<2y$
for all
![]() $n \in \mathbb {N}$
.
$n \in \mathbb {N}$
.
To complete the proof, it will be enough to show that
![]() $2y\le 4^{X^{3^{k+1}}}$
. For this, define
$2y\le 4^{X^{3^{k+1}}}$
. For this, define
![]() $X_n:=X^{3^n}$
for all
$X_n:=X^{3^n}$
for all
![]() $n\ge 0$
and note that, thanks to Corollary 2.4, we have
$n\ge 0$
and note that, thanks to Corollary 2.4, we have
 $$ \begin{align*} \prod_{X_n<p\le X_n^3}\bigg(1-\frac{1}{p}\bigg)<\frac{1}{2} \quad \text{for all }n\ge 0. \end{align*} $$
$$ \begin{align*} \prod_{X_n<p\le X_n^3}\bigg(1-\frac{1}{p}\bigg)<\frac{1}{2} \quad \text{for all }n\ge 0. \end{align*} $$
By the definition of
![]() $r_j$
, it follows that
$r_j$
, it follows that
Lastly, since
![]() $\prod _{p\le x}p<4^x$
for all
$\prod _{p\le x}p<4^x$
for all
![]() $x\ge 1$
(see, for example, [Reference De Koninck and Luca2, Lemma 2.8]), we conclude that
$x\ge 1$
(see, for example, [Reference De Koninck and Luca2, Lemma 2.8]), we conclude that
 $$ \begin{align*} 2y \le 2\prod_{j=0}^k q_j \le \prod_{i=1}^{r_{k+1}}p_i \le \prod_{p\le X_{k+1}}p\le 4^{X_{k+1}}. \end{align*} $$
$$ \begin{align*} 2y \le 2\prod_{j=0}^k q_j \le \prod_{i=1}^{r_{k+1}}p_i \le \prod_{p\le X_{k+1}}p\le 4^{X_{k+1}}. \end{align*} $$
Therefore,
![]() $x_n \le 4^{X_{k+1}}$
for all
$x_n \le 4^{X_{k+1}}$
for all
![]() $n \in \mathbb {N}$
.
$n \in \mathbb {N}$
.
Acknowledgement
The authors are thankful to the anonymous referee for a careful reading of the manuscript and for suggesting the open questions stated at the end of Section 1.