No CrossRef data available.
Article contents
ON THE CENTRE OF THE AUTOMORPHISM GROUP OF A GROUP
Published online by Cambridge University Press: 16 June 2015
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
If the centre of a group 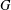 $G$ is trivial, then so is the centre of its automorphism group. We study the structure of the centre of the automorphism group of a group
$G$ is trivial, then so is the centre of its automorphism group. We study the structure of the centre of the automorphism group of a group 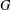 $G$ when the centre of
$G$ when the centre of 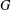 $G$ is a cyclic group. In particular, it is shown that the exponent of
$G$ is a cyclic group. In particular, it is shown that the exponent of 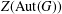 $Z(\text{Aut}(G))$ is less than or equal to the exponent of
$Z(\text{Aut}(G))$ is less than or equal to the exponent of 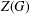 $Z(G)$ in this case.
$Z(G)$ in this case.
MSC classification
Primary:
20F28: Automorphism groups of groups
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 92 , Issue 3 , December 2015 , pp. 390 - 396
- Copyright
- © 2015 Australian Mathematical Publishing Association Inc.
References
Adney, J. E. and Yen, T., ‘Automorphisms of a p-group’, Illinois J. Math. 9 (1965), 137–143.CrossRefGoogle Scholar
Deaconescu, M. and Walls, G. L., ‘On the group of automorphisms of a group’, Amer. Math. Monthly 118(5) (2011), 452–455.CrossRefGoogle Scholar
Formanek, E., ‘Fixed points and centers of automorphism groups of free nilpotent groups’, Comm. Algebra 30(2) (2002), 1033–1038.CrossRefGoogle Scholar

