Article contents
On powerful and p-central restricted Lie algebras
Published online by Cambridge University Press: 17 April 2009
Extract
In this note we analyse the analogy between m-potent and p-central restricted Lie algebras and p-groups. For restricted Lie algebras the notion of m-potency has stronger implications than for p-groups (Theorem A). Every finite-dimensional restricted Lie algebra is isomorphic to 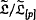 for some finite-dimensional p-central restricted Lie algebra
for some finite-dimensional p-central restricted Lie algebra 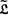 (Proposition B). In particular, for restricted Lie algebras there does not hold an analogue of J.Buckley's theorem. For p odd one can characterise powerful restricted Lie algebras in terms of the cup product map in the same way as for finite p-groups (Theorem C). Moreover, the p-centrality of the finite-dimensional restricted Lie algebra has a strong implication on the structure of the cohomology ring H•(,) (Theorem D).
(Proposition B). In particular, for restricted Lie algebras there does not hold an analogue of J.Buckley's theorem. For p odd one can characterise powerful restricted Lie algebras in terms of the cup product map in the same way as for finite p-groups (Theorem C). Moreover, the p-centrality of the finite-dimensional restricted Lie algebra has a strong implication on the structure of the cohomology ring H•(,) (Theorem D).
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 2007
References
- 1
- Cited by

