Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-11T10:04:49.272Z Has data issue: false hasContentIssue false
  • English
  • Français

ON p-ADIC INTERPOLATION IN TWO OF MAHLER’S PROBLEMS

Part of: Diophantine approximation, transcendental number theory Algebraic number theory: local and $p$-adic fields

Published online by Cambridge University Press:  22 September 2022

BRUNO DE PAULA MIRANDA Open the ORCID record for BRUNO DE PAULA MIRANDA [Opens in a new window]  and
JEAN LELIS Open the ORCID record for JEAN LELIS [Opens in a new window]
BRUNO DE PAULA MIRANDA
Affiliation:
Instituto Federal de Goiás, Avenida Saia Velha, Km 6, BR-040, s/n, Parque Esplanada V, Valparaíso de Goiás, GO 72876-601, Brazil e-mail: bruno.miranda@ifg.edu.br
JEAN LELIS*
Affiliation:
Faculdade de Matemática, Instituto de Ciências Exatas e Naturais, Universidade Federal do Pará, Belém PA, Brazil
*
e-mail: jeanlelis@ufpa.br
Get access Rights & Permissions [Opens in a new window]

Abstract

Motivated by the p-adic approach in two of Mahler’s problems, we obtain some results on p-adic analytic interpolation of sequences of integers 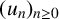$(u_n)_{n\geq 0}$. We show that if 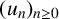$(u_n)_{n\geq 0}$ is a sequence of integers with 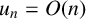$u_n = O(n)$ which can be p-adically interpolated by an analytic function 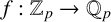$f:\mathbb {Z}_p\rightarrow \mathbb {Q}_p$, then 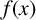$f(x)$ is a polynomial function of degree at most one. The case 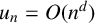$u_n=O(n^d)$ with 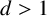$d>1$ is also considered with additional conditions. Moreover, if X and Y are subsets of 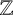$\mathbb {Z}$ dense in 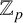$\mathbb {Z}_p$, we prove that there are uncountably many p-adic analytic injective functions 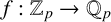$f:\mathbb {Z}_p\to \mathbb {Q}_p$, with rational coefficients, such that 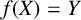$f(X)=Y$.

Keywords

p-adic interpolationp-adic analytic functionMahler expansionStrassmann’s theoremp-adic Liouville number

MSC classification

Primary: 11J61: Approximation in non-Archimedean valuations
Secondary: 11S80: Other analytic theory (analogues of beta and gamma functions, $p$-adic integration, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 108 , Issue 1 , August 2023 , pp. 69 - 80
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bell, J. P., ‘A generalised Skolem–Mahler–Lech theorem for affine varieties’, J. Lond. Math. Soc. (2) 73(2) (2006), 367–379.CrossRefGoogle Scholar
Bihani, P., Sheppard, W. P. and Young, P. T., ‘ $p$ -Adic interpolation of the Fibonacci sequence via hypergeometric functions’, Fibonacci Quart. 43(3) (2005), 213–226.Google Scholar
Clark, D., ‘A note on the $p$ -adic convergence of the solutions of linear differential equations’, Proc. Amer. Math. Soc. 17 (1966), 262–269.Google Scholar
Georg, F., ‘Ueber arithmetische Eingenschaften analytischer Functionen’, Math. Ann. 58(4) (1904), 545–557.Google Scholar
Lelis, J. and Marques, D., ‘Some results on arithmetic properties of $p$ -adic Liouville numbers’. p-Adic Numbers Ultrametric Anal. Appl. 11(3) (2019), 216–222.CrossRefGoogle Scholar
Lelis, J. and Marques, D., ‘On transcendental entire functions mapping $\mathbb{Q}$ into itself’, J. Number Theory 206 (2020), 310–319.CrossRefGoogle Scholar
Mahler, K., ‘An interpolation series for continuous functions of a $p$ -adic variable’, J. reine angew. Math. 199 (1958), 23–34.CrossRefGoogle Scholar
Mahler, K., Lectures on Transcendental Numbers, Lecture Notes in Mathematics, 546 (Springer-Verlag, Berlin, 1976).CrossRefGoogle Scholar
Mahler, K., ‘Some suggestions for further research,’ Bull. Aust. Math. Soc. 29(1) (1984), 101–108.CrossRefGoogle Scholar
Maillet, E., Introduction à la Théorie des Nombres Transcendants et des Propriétés Arithmétiques des Fonctions (Gauthier–Villars, Paris, 1906).Google Scholar
Marques, D. and Moreira, C. G., ‘On a variant of a question proposed by K. Mahler concerning Liouville numbers’, Bull. Aust. Math. Soc. 91 (2015), 29–33.CrossRefGoogle Scholar
Marques, D. and Moreira, C. G., ‘A positive answer for a question proposed by K. Mahler’, Math. Ann. 368 (2017), 1059–1062.CrossRefGoogle Scholar
Marques, D. and Moreira, C. G., ‘On a stronger version of a question proposed by K. Mahler’, J. Number Theory 194 (2019), 372–380.CrossRefGoogle Scholar
Murty, M. R., Introduction to $p$ -Adic Analytic Number Theory, Studies in Advanced Mathematics, 27 (American Mathematical Society, Providence, RI, 2009).Google Scholar
Robert, A. M., A Course in $p$ -Adic Analysis, Graduate Texts in Mathematics, 198 (Springer, New York, 2013).Google Scholar
Rowland, E. and Yassawi, E., ‘ $p$ -Adic asymptotic properties of constant-recursive sequences’, Indag. Math. (N.S.) 28(1) (2017), 205–220.CrossRefGoogle Scholar
Schikhof, W. H., Ultrametric Calculus (Cambridge University Press, Cambridge, 2006).Google Scholar
Stäckel, P., ‘Arithmetische eingenschaften analytischer Functionen’, Acta Math. 25 (1902), 371–383.CrossRefGoogle Scholar