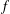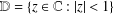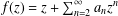Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Maleki, Zahra
Shams, Saeid
Ebadian, Ali
and
Analouei Adegani, Ebrahim
2020.
On Some Problems of Strongly Ozaki Close-to-Convex Functions.
Journal of Function Spaces,
Vol. 2020,
Issue. ,
p.
1.
SIM, YOUNG JAE
and
THOMAS, DEREK K.
2021.
ON THE DIFFERENCE OF COEFFICIENTS OF OZAKI CLOSE-TO-CONVEX FUNCTIONS.
Bulletin of the Australian Mathematical Society,
Vol. 103,
Issue. 1,
p.
124.
Sim, Young Jae
Lecko, Adam
and
Thomas, Derek K.
2021.
The second Hankel determinant for strongly convex and Ozaki close-to-convex functions.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 200,
Issue. 6,
p.
2515.
Allu, Vasudevarao
Lecko, Adam
and
Thomas, Derek K.
2022.
Hankel, Toeplitz, and Hermitian-Toeplitz Determinants for Certain Close-to-convex Functions.
Mediterranean Journal of Mathematics,
Vol. 19,
Issue. 1,
Hu, Zhenyong
Fan, Jinhua
Wang, Xiaoyuan
and
Srivastava, H. M.
2023.
A Study of the Higher-Order Schwarzian Derivatives of Hirotaka Tamanoi.
Mathematica Slovaca,
Vol. 73,
Issue. 4,
p.
921.
Sümer Eker, Sevtap
Lecko, Adam
Çekiç, Bilal
and
Şeker, Bilal
2023.
The Second Hankel Determinant of Logarithmic Coefficients for Strongly Ozaki Close-to-Convex Functions.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 46,
Issue. 6,
Shi, Lei
and
Arif, Muhammad
2023.
Sharp bounds on the third Hankel determinant for the Ozaki close-to-convex and convex functions.
Lithuanian Mathematical Journal,
Vol. 63,
Issue. 4,
p.
487.
Kumar, Virendra
and
Cho, Nak Eun
2023.
Moduli difference of successive inverse and logarithmic coefficients for a class of close-to-convex functions.
Asian-European Journal of Mathematics,
Vol. 16,
Issue. 03,
Sharma, Prathviraj
Alharbi, Asma
Sivasubramanian, Srikandan
and
El-Deeb, Sheza M.
2024.
On Ozaki Close-to-Convex Functions with Bounded Boundary Rotation.
Symmetry,
Vol. 16,
Issue. 7,
p.
839.
Vijaya, Kaliappan
Murugusundaramoorthy, Gangadharan
Breaz, Daniel
Oros, Georgia Irina
and
El-Deeb, Sheza M.
2024.
Ozaki-Type Bi-Close-to-Convex and Bi-Concave Functions Involving a Modified Caputo’s Fractional Operator Linked with a Three-Leaf Function.
Fractal and Fractional,
Vol. 8,
Issue. 4,
p.
220.
Kumar, Sushil
Pandey, Rakesh Kumar
and
Rai, Pratima
2024.
Certain sharp estimates of Ozaki close-to-convex functions.
Asian-European Journal of Mathematics,
Vol. 17,
Issue. 06,