Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-11T17:55:40.116Z Has data issue: false hasContentIssue false
  • English
  • Français

ON MINIMAL RESTRICTED ASYMPTOTIC BASES

Part of: Sequences and sets

Published online by Cambridge University Press:  06 October 2022

LINBO SHANG Open the ORCID record for LINBO SHANG [Opens in a new window] ,
DENGRONG LING Open the ORCID record for DENGRONG LING [Opens in a new window]  and
MIN TANG Open the ORCID record for MIN TANG [Opens in a new window]
LINBO SHANG
Affiliation:
School of Mathematics and Statistics, Anhui Normal University, Wuhu 241003, PR China e-mail: ashanglinbo@163.com
DENGRONG LING
Affiliation:
School of Mathematics and Statistics, Anhui Normal University, Wuhu 241003, PR China e-mail: lingdengrong@163.com
MIN TANG*
Affiliation:
School of Mathematics and Statistics, Anhui Normal University, Wuhu 241003, PR China
*
e-mail: tmzzz2000@163.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 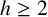$h \geq 2$ be a positive integer. We introduce the concept of minimal restricted asymptotic bases and obtain some examples of minimal restricted asymptotic bases of order h.

Keywords

minimal asymptotic basisminimal restricted asymptotic basis

MSC classification

Primary: 11B13: Additive bases, including sumsets
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 107 , Issue 3 , June 2023 , pp. 368 - 373
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported by the National Natural Science Foundation of China (Grant No. 11971033), Top Talents Project of Anhui Department of Education (Grant No. gxbjZD05) and Key Project of Anhui Department of Education (Grant No. KJ2021A0099).

References

Alladi, K. and Krantz, S., ‘Reflections on Paul Erdős on his birth centenary’, Notices Amer. Math. Soc. 62 (2015), 121–143.Google Scholar
Chen, Y. G. and Tang, M., ‘On a problem of Nathanson’, Acta Arith. 185 (2018), 275–280.10.4064/aa171031-26-4CrossRefGoogle Scholar
Jańczak, M. and Schoen, T., ‘Dense minimal asymptotic bases of order two’, J. Number Theory 130 (2010), 580–585.10.1016/j.jnt.2009.09.010CrossRefGoogle Scholar
Nathanson, M. B., ‘Minimal bases and maximal nonbases in additive number theory’, J. Number Theory 6 (1974), 324–333.10.1016/0022-314X(74)90028-6CrossRefGoogle Scholar
Nathanson, M. B., ‘Cassels bases’, in: Additive Number Theory (eds. Chudnovsky, D. and Chudnovsky, G.) (Springer, New York, 2010), 259–285.10.1007/978-0-387-68361-4_19CrossRefGoogle Scholar
Nathanson, M. B., ‘A new class of minimal asymptotic bases’, Preprint, 2022, arXiv:2006.14562v2.CrossRefGoogle Scholar
Sun, C. F., ‘On a problem of Nathanson on minimal asymptotic bases’, J. Number Theory 218 (2021), 152–160.10.1016/j.jnt.2020.07.014CrossRefGoogle Scholar
Sun, C. F. and Tao, T. T., ‘On $g$ -adic minimal asymptotic bases of order $h$ ’, Int. J. Number Theory 15 (2019), 389–406.10.1142/S1793042119500209CrossRefGoogle Scholar