Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-27T00:08:51.171Z Has data issue: false hasContentIssue false
  • English
  • Français

ON 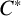$\mathbf{\mathit{C}}^{*}$-ALGEBRAS WHICH DETECT NUCLEARITY

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  05 May 2022

FLORIN POP Open the ORCID record for FLORIN POP [Opens in a new window]
FLORIN POP*
Affiliation:
Department of Mathematics, Wagner College, Staten Island, NY 10301, USA
*
e-mail: fpop@wagner.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

A 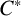$C^{*}$ -algebra A is said to detect nuclearity if, whenever a 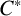$C^{*}$ -algebra B satisfies 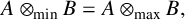$A\otimes _{\mathrm{min}} B = A\otimes _{\mathrm{max}} B,$ it follows that B is nuclear. In this note, we survey the main results associated with this topic and present the background and tools necessary for proving the main results. In particular, we show that the 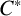$C^{*}$ -algebra 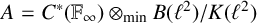$A = C^{*}(\mathbb {F}_{\infty })\otimes _{\mathrm{min}} B(\ell ^{2})/K(\ell ^{2})$ detects nuclearity. This result is known to experts, but has never appeared in the literature.

Keywords

C*-algebratensor productnuclear

MSC classification

Primary: 46L06: Tensor products of $C^*$-algebras
Secondary: 46L05: General theory of $C^*$-algebras
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 107 , Issue 1 , February 2023 , pp. 125 - 133
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Choi, M. D. and Effros, E. G., ‘The completely positive lifting problem for ${C}^{\ast }$ -algebras’, Ann. of Math. (2) 104 (1976), 585–609.10.2307/1970968CrossRefGoogle Scholar
Courtney, K. E., ‘Universal ${C}^{\ast }$ -algebras with the local lifting property’, Math. Scand. 127 (2021), 361–381.CrossRefGoogle Scholar
Harris, S. J. and Kim, S.-J., ‘Crossed products of operator systems’, J. Funct. Anal. 276 (2019), 2156–2193.10.1016/j.jfa.2018.11.017CrossRefGoogle Scholar
Kavruk, A., ‘On a non-commutative analogue of a classical result of Namioka and Phelps’, J. Funct. Anal. 269 (2015), 3282–3303.CrossRefGoogle Scholar
Kirchberg, E., ‘The Fubini theorem for exact ${C}^{\ast }$ -algebras’, J. Operator Theory 10 (1983), 3–8.Google Scholar
Kirchberg, E., ‘On nonsemisplit extensions, tensor products and exactness of group ${C}^{\ast }$ -algebras’, Invent. Math. 112 (1993), 449–489.CrossRefGoogle Scholar
Kirchberg, E., ‘Commutants of unitaries in UHF algebras and functorial properties of exactness’, J. reine angew. Math. 452 (1994), 39–77.Google Scholar
Kirchberg, E. and Wassermann, S., ‘ ${C}^{\ast }$ -algebras generated by operator systems’, J. Funct. Anal. 155 (1998), 324–351.10.1006/jfan.1997.3226CrossRefGoogle Scholar
Lance, E. C., ‘On nuclear ${C}^{\ast }$ -algebras’, J. Funct. Anal. 12 (1973), 157–176.CrossRefGoogle Scholar
Paulsen, V. I., Completely Bounded Maps and Operator Algebras (Cambridge University Press, Cambridge, 2003).CrossRefGoogle Scholar
Pisier, G., Tensor Products of ${C}^{\ast }$ -Algebras and Operator Spaces: The Connes–Kirchberg Problem, London Mathematical Society Student Texts, 96 (Cambridge University Press, Cambridge, 2020).Google Scholar
Pop, F., ‘Remarks on the completely bounded approximation property for ${C}^{\ast }$ -algebras,’ Houston J. Math. 43 (2017), 937–945.Google Scholar