No CrossRef data available.
Article contents
ON KLEINIAN GROUPS WITH THE SAME SET OF AXES
Published online by Cambridge University Press: 01 December 2008
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
J. W. Anderson (1996) asked whether two finitely generated Kleinian groups 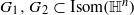 with the same set of axes are commensurable. We give some partial solutions.
with the same set of axes are commensurable. We give some partial solutions.
MSC classification
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 78 , Issue 3 , December 2008 , pp. 437 - 441
- Copyright
- Copyright © 2009 Australian Mathematical Society
References
[1]Anderson, J. W., ‘The limit set intersection theorem for finitely generated Kleinian groups’, Math. Res. Lett. 3 (1996), 675–692.CrossRefGoogle Scholar
[4]Bestvina, M., Questions in geometric group theory, 2004,http://www.math.utah.edu/∼bestvina/eprints/questions-updated.pdf.Google Scholar
[5]Hempel, J., ‘The finitely generated intersection property for Kleinian groups’, in: Knot Theory and Manifolds, Lectures Notes in Mathematics, 1144 (Springer, Berlin, 1985), pp. 18–24.CrossRefGoogle Scholar
[6]Long, D. D. and Reid, A. W., ‘On Fuchsian groups with the same set of axes’, Bull. London Math. Soc. 30 (1998), 533–538.CrossRefGoogle Scholar
[8]Ratcliffe, J. G., Foundations of Hyperbolic Manifolds (Springer, New York, 1994).CrossRefGoogle Scholar
[9]Susskind, P., ‘An infinitely generated intersection of the hyperbolic group’, Proc. Amer. Math. Soc. 129 (2001), 2643–2646.CrossRefGoogle Scholar
[10]Susskind, P. and Swarup, G., ‘Limit sets of geometrically finite hyperbolic groups’, Amer. J. Math. 114 (1992), 233–250.CrossRefGoogle Scholar

