No CrossRef data available.
Article contents
ON EXPONENTIAL DIOPHANTINE EQUATIONS CONTAINING THE EULER QUOTIENT
Part of:
Diophantine equations
Published online by Cambridge University Press: 14 October 2014
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let  $a$ and
$a$ and 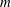 $m$ be relatively prime positive integers with
$m$ be relatively prime positive integers with 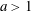 $a>1$ and
$a>1$ and 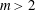 $m>2$. Let
$m>2$. Let 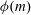 ${\it\phi}(m)$ be Euler’s totient function. The quotient
${\it\phi}(m)$ be Euler’s totient function. The quotient 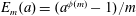 $E_{m}(a)=(a^{{\it\phi}(m)}-1)/m$ is called the Euler quotient of
$E_{m}(a)=(a^{{\it\phi}(m)}-1)/m$ is called the Euler quotient of 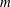 $m$ with base
$m$ with base  $a$. By Euler’s theorem,
$a$. By Euler’s theorem, 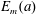 $E_{m}(a)$ is an integer. In this paper, we consider the Diophantine equation
$E_{m}(a)$ is an integer. In this paper, we consider the Diophantine equation 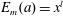 $E_{m}(a)=x^{l}$ in integers
$E_{m}(a)=x^{l}$ in integers 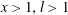 $x>1,l>1$. We conjecture that this equation has exactly five solutions
$x>1,l>1$. We conjecture that this equation has exactly five solutions 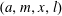 $(a,m,x,l)$ except for
$(a,m,x,l)$ except for 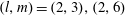 $(l,m)=(2,3),(2,6)$, and show that if the equation has solutions, then
$(l,m)=(2,3),(2,6)$, and show that if the equation has solutions, then 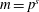 $m=p^{s}$ or
$m=p^{s}$ or 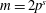 $m=2p^{s}$ with
$m=2p^{s}$ with 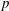 $p$ an odd prime and
$p$ an odd prime and 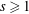 $s\geq 1$.
$s\geq 1$.
MSC classification
Primary:
11D61: Exponential equations
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © 2014 Australian Mathematical Publishing Association Inc.
References
Agoh, T., Dilcher, K. and Skula, L., ‘Fermat quotients for composite moduli’, J. Number Theory 66 (1997), 29–50.CrossRefGoogle Scholar
Bennett, M. A. and Skinner, C., ‘Ternary Diophantine equations via Galois representations and modular forms’, Canad. J. Math. 56 (2004), 23–54.Google Scholar
Bennett, M. A., Vatsal, V. and Yazdani, S., ‘Ternary Diophantine equations of signature (p, p, 3)’, Compositio Math. 140 (2004), 1399–1416.CrossRefGoogle Scholar
Bosma, W. and Cannon, J., Handbook of Magma Functions, Department of Mathematics, University of Sydney, available online at http://magma.maths.usyd.edu.au/magma/.Google Scholar
Cao, Z., ‘The Diophantine equations x 4 − y 4 = z p and x 4 − 1 = d y q’, C. R. Math. Rep. Acad. Sci. Can. 21 (1999), 23–27.Google Scholar
Cohn, J.H.E., ‘The Diophantine equations x 4 − D y 2 = 1, II’, Acta Arith. 78 (1996/1997), 401–403.CrossRefGoogle Scholar
Kihel, O. and Levesque, C., ‘On a few Diophantine equations related to Fermat’s last theorem’, Canad. Math. Bull. 45 (2002), 247–256.Google Scholar
Le, M. H., ‘A note on the Diophantine equation x p−1 − 1 = p y q’, C. R. Math. Rep. Acad. Sci. Can. 15 (1993), 121–124.Google Scholar
Ljunggren, W., ‘Zur Theorie der Gleichung x 2 + 1 = D y 4’, Avh. Norske Vid. Akad. Oslo 5 (1942), 1–27.Google Scholar
Lucas, E., Théorie des nombres (Gauthier-Villars, Paris, 1891), reprinted (A. Blanchard, Paris, 1961).Google Scholar
Mihilescu, P., ‘Primary cyclotomic units and a proof of Catalan’s conjecture’, J. reine angew. Math. 572 (2004), 167–195.Google Scholar
Osada, H. and Terai, N., ‘Generalization of Lucas’ Theorem for Fermat’s quotient’, C. R. Math. Rep. Acad. Sci. Can. 11 (1989), 115–120.Google Scholar
Störmer, C., ‘L’équation m arctan1∕x + n arctan1∕y = k𝜋∕4’, Bull. Soc. Math. France 27 (1899), 160–170.CrossRefGoogle Scholar
Terai, N., ‘Generalization of Lucas’ Theorem for Fermat’s quotient II’, Tokyo J. Math. 13 (1990), 277–287.Google Scholar

