No CrossRef data available.
Article contents
ON AN INTEGRAL OF 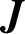 $\boldsymbol {J}$-BESSEL FUNCTIONS AND ITS APPLICATION TO MAHLER MEASURE
$\boldsymbol {J}$-BESSEL FUNCTIONS AND ITS APPLICATION TO MAHLER MEASURE
Published online by Cambridge University Press: 09 July 2021
Abstract
Cogdell et al. [‘Evaluating the Mahler measure of linear forms via Kronecker limit formulas on complex projective space’, Trans. Amer. Math. Soc. (2021), to appear] developed infinite series representations for the logarithmic Mahler measure of a complex linear form with four or more variables. We establish the case of three variables by bounding an integral with integrand involving the random walk probability density 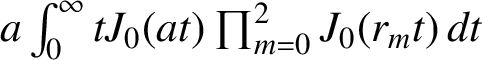 $a\int _0^\infty tJ_0(at) \prod _{m=0}^2 J_0(r_m t)\,dt$, where
$a\int _0^\infty tJ_0(at) \prod _{m=0}^2 J_0(r_m t)\,dt$, where 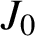 $J_0$ is the order-zero Bessel function of the first kind and a and
$J_0$ is the order-zero Bessel function of the first kind and a and 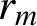 $r_m$ are positive real numbers. To facilitate our proof we develop an alternative description of the integral’s asymptotic behaviour at its known points of divergence. As a computational aid for numerical experiments, an algorithm to calculate these series is presented in the appendix.
$r_m$ are positive real numbers. To facilitate our proof we develop an alternative description of the integral’s asymptotic behaviour at its known points of divergence. As a computational aid for numerical experiments, an algorithm to calculate these series is presented in the appendix.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © 2021 Australian Mathematical Publishing Association Inc.
Footnotes
The authors acknowledge the support of NSF grant DMS-1820731.
The views expressed in this article are the author’s own and not those of the United States Merchant Marine Academy, the Maritime Administration, the Department of Transportation or the United States government.


