No CrossRef data available.
Article contents
A NOTE ON THE POLIGNAC NUMBERS
Published online by Cambridge University Press: 13 March 2014
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Suppose that 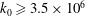 $k_0\geq 3.5\times 10^6$ and
$k_0\geq 3.5\times 10^6$ and 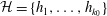 $\mathcal{H}=\{h_1,\ldots,h_{k_0}\}$ is admissible. Then, for any
$\mathcal{H}=\{h_1,\ldots,h_{k_0}\}$ is admissible. Then, for any 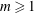 $m\geq 1$, the set
$m\geq 1$, the set 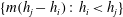 $\{m(h_j-h_i):\, h_i<h_j\}$ contains at least one Polignac number.
$\{m(h_j-h_i):\, h_i<h_j\}$ contains at least one Polignac number.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © 2014 Australian Mathematical Publishing Association Inc.
References
Motohashi, Y. and Pintz, J., ‘A smoothed GPY sieve’, Bull. Lond. Math. Soc. 40 (2008), 298–310.CrossRefGoogle Scholar
Pintz, J., ‘Polignac numbers, conjectures of Erdős on gaps between primes, arithmetic progressions in primes, and the bounded gap conjecture’, Preprint, arXiv:1305.6289.Google Scholar
de Polignac, A., ‘Six propositions arithmologiques déduites du crible d’Ératosthène’, Nouv. Ann. Math. 8 (1849), 423–429.Google Scholar
Zhang, Y., ‘Bounded gaps between primes’, Ann. of Math. (2), to appear.Google Scholar

