Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Dung, Nguyen Van
and
Hang, Vo Thi Le
2018.
The generalized hyperstability of general linear equations in quasi-Banach spaces.
Journal of Mathematical Analysis and Applications,
Vol. 462,
Issue. 1,
p.
131.
Van Dung, Nguyen
and
Le Hang, Vo Thi
2018.
Stability of a mixed additive and quadratic functional equation in quasi-Banach spaces.
Journal of Fixed Point Theory and Applications,
Vol. 20,
Issue. 3,
Ding, Yali
and
Xu, Tian-Zhou
2019.
Approximate solution of generalized inhomogeneous radical quadratic functional equations in 2-Banach spaces.
Journal of Inequalities and Applications,
Vol. 2019,
Issue. 1,
Kang, Dongseung
and
Kim, Hoewoon B.
2019.
On a New Stability Problem of Radical nth-Degree Functional Equation by Brzdęk’s Fixed-Point Method.
Journal of Function Spaces,
Vol. 2019,
Issue. ,
p.
1.
Dung, Nguyen Van
and
Sintunavarat, Wutiphol
2019.
Ulam Type Stability.
p.
97.
Aiemsomboon, Laddawan
and
Sintunavarat, Wutiphol
2020.
On New Approximations for Generalized Cauchy Functional Equations Using Brzdęk and Ciepliński’s Fixed Point Theorems in 2-Banach Spaces.
Acta Mathematica Scientia,
Vol. 40,
Issue. 3,
p.
824.
Ciepliński, Krzysztof
2021.
Ulam stability of functional equations in 2-Banach spaces via the fixed point method.
Journal of Fixed Point Theory and Applications,
Vol. 23,
Issue. 3,
Sharma, Ravinder Kumar
and
Chandok, Sumit
2022.
The Generalized Hyperstability of General Linear Equation in Quasi-2-Banach Space.
Acta Mathematica Scientia,
Vol. 42,
Issue. 4,
p.
1357.
Sharma, Ravinder Kumar
and
Chandok, Sumit
2022.
Ulam stability of a quadratic-type functional equation in 3 variables in the quasi-Banach space.
Functiones et Approximatio Commentarii Mathematici,
Vol. -1,
Issue. -1,
Ciepliński, Krzysztof
2023.
On perturbations of two general equations in several variables.
Mathematische Annalen,
Vol. 385,
Issue. 1-2,
p.
921.
Park, Choonkil
and
Senasukh, Jedsada
2023.
Stability of an (A,Q)-functional equation in a Banach space.
Asian-European Journal of Mathematics,
Vol. 16,
Issue. 10,
Sharma, Ravinder Kumar
Chandok, Sumit
and
Dey, Bikash Koli
2023.
Equivalence for Various Forms of Quadratic Functional Equations and Their Generalized Hyers–Ulam–Rassias Stability.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2023,
Issue. 1,
El Fatini, Mohamed
Almahalebi, Muaadh
Park, Choonkil
and
Alghamdii, Ahmad M.
2025.
Hyperstability of a quadratic functional equation with involutions in ultrametric n-Banach spaces via fixed point approach.
The Journal of Analysis,
Vol. 33,
Issue. 5,
p.
2205.
Boutarfass, Jawad
EL-Fassi, Iz-iddine
and
Oukhtite, Lahcen
2025.
A new approach to approximate the solution of two general functional equations in quasi-Banach spaces.
Bulletin des Sciences Mathématiques,
Vol. 199,
Issue. ,
p.
103564.
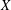 $X$ and
$X$ and 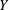 $Y$ be two normed spaces over fields
$Y$ be two normed spaces over fields 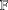 $\mathbb{F}$ and
$\mathbb{F}$ and 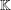 $\mathbb{K}$ , respectively. We prove new generalised hyperstability results for the general linear equation of the form
$\mathbb{K}$ , respectively. We prove new generalised hyperstability results for the general linear equation of the form 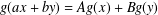 $g(ax+by)=Ag(x)+Bg(y)$ , where
$g(ax+by)=Ag(x)+Bg(y)$ , where 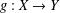 $g:X\rightarrow Y$ is a mapping and
$g:X\rightarrow Y$ is a mapping and 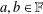 $a,b\in \mathbb{F}$ ,
$a,b\in \mathbb{F}$ , 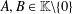 $A,B\in \mathbb{K}\backslash \{0\}$ , using a modification of the method of Brzdęk [‘Stability of additivity and fixed point methods’, Fixed Point Theory Appl.2013 (2013), Art. ID 285, 9 pages]. The hyperstability results of Piszczek [‘Hyperstability of the general linear functional equation’, Bull. Korean Math. Soc.52 (2015), 1827–1838] can be derived from our main result.
$A,B\in \mathbb{K}\backslash \{0\}$ , using a modification of the method of Brzdęk [‘Stability of additivity and fixed point methods’, Fixed Point Theory Appl.2013 (2013), Art. ID 285, 9 pages]. The hyperstability results of Piszczek [‘Hyperstability of the general linear functional equation’, Bull. Korean Math. Soc.52 (2015), 1827–1838] can be derived from our main result.
