Article contents
A NOTE ON THE DIOPHANTINE EQUATION 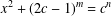 $x^{2}+(2c-1)^{m}=c^{n}$
$x^{2}+(2c-1)^{m}=c^{n}$
Published online by Cambridge University Press: 12 July 2018
Abstract
Let 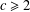 $c\geq 2$ be a positive integer. Terai [‘A note on the Diophantine equation
$c\geq 2$ be a positive integer. Terai [‘A note on the Diophantine equation 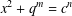 $x^{2}+q^{m}=c^{n}$’, Bull. Aust. Math. Soc.90 (2014), 20–27] conjectured that the exponential Diophantine equation
$x^{2}+q^{m}=c^{n}$’, Bull. Aust. Math. Soc.90 (2014), 20–27] conjectured that the exponential Diophantine equation  $x^{2}+(2c-1)^{m}=c^{n}$ has only the positive integer solution
$x^{2}+(2c-1)^{m}=c^{n}$ has only the positive integer solution 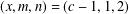 $(x,m,n)=(c-1,1,2)$. He proved his conjecture under various conditions on
$(x,m,n)=(c-1,1,2)$. He proved his conjecture under various conditions on  $c$ and
$c$ and 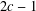 $2c-1$. In this paper, we prove Terai’s conjecture under a wider range of conditions on
$2c-1$. In this paper, we prove Terai’s conjecture under a wider range of conditions on  $c$ and
$c$ and 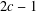 $2c-1$. In particular, we show that the conjecture is true if
$2c-1$. In particular, we show that the conjecture is true if 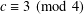 $c\equiv 3\hspace{0.6em}({\rm mod}\hspace{0.2em}4)$ and
$c\equiv 3\hspace{0.6em}({\rm mod}\hspace{0.2em}4)$ and 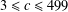 $3\leq c\leq 499$.
$3\leq c\leq 499$.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 98 , Issue 2 , October 2018 , pp. 188 - 195
- Copyright
- © 2018 Australian Mathematical Publishing Association Inc.
Footnotes
This research was supported by the National Natural Science Foundation of China (grant no. 11601108) and the Natural Science Foundation of Hainan Province (grant no. 20161002).
References
- 5
- Cited by

