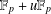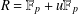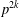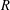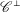Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
SHI, Minjia
TANG, Jie
and
GE, Maorong
2017.
Note on Support Weight Distribution of Linear Codes over $\mathbb{F}_{p}+u\mathbb{F}_{p}+v\mathbb{F}_{p}+uv\mathbb{F}_{p}$.
IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences,
Vol. E100.A,
Issue. 6,
p.
1346.
SHI, MINJIA
FENG, JIAQI
GAO, JIAN
ALAHMADI, ADEL
and
SOLÉ, PATRICK
2017.
ON THE SUPPORT WEIGHT DISTRIBUTION OF LINEAR CODES OVER THE RING .
Bulletin of the Australian Mathematical Society,
Vol. 95,
Issue. 1,
p.
157.